数据结构笔记（桂电教材版本）

写在前面

这个课是以前从来没接触过的东西，而且一直学 web，太久没接触 c 语言了，第一节课看到 for 循环甚至有点陌生，学得有点吃力，所以必须整点笔记，记下相关概念、知识点和平时学习过程中的问题和思考，期末复习用

2022.1.23

没想到我这笔记还能留到考研用，属于是未雨绸缪了

第一章 绪论

• 数据结构研究：数据的逻辑结构（数据内部之间的构成方法）、数据的物理储存（数据在内存里面怎么存的）、数据的操作实现（用什么语言写，用什么算法实现）三方面的问题

抽象数据类型（Abstract Data Type，ADT）

一个数学模型以及定义在该模型上的一组操作，强调对数据类型的抽象，不讲究具体实现

作用：目的在于隐藏运算实现的细节和内部数据结构，同时向用户提供该数据类型的接口

应用程序编程接口（Application Program Interface，API）

把实现和使用分离，把编程模块化，函数封装成的库就是一个典型的API接口，只管用，一般不用管这个库是怎么写的，这也是面向对象编程的一个重要思维

数据结构

行话

• 数据：信息的载体，能够被计算机程序处理的一些符号（字符、数字、声音和图像等等）
• 数据元素/结点：组成数据的基本单位
• 数据项：==是数据的最小单位==，是数据元素的组成单位，比它还小
• 数据结构：存在相互关系的数据元素的集合，开发者会根据这种数据结构设计相应的算法，确保运算以后的新结构依旧保持原来的结构类型
• 数据对象：是必须由软件理解的复合信息表示，跟上面四个东西没有很强的逻辑关系，数据对象描述包括了其所有的属性，只用来封装数据，不对数据进行操作

---

整点自己的理解

假如有两张表，一个是课程表，一个是憨憨弱口令表，那么这两张表就是==数据==

课程代号	课程名字	授课老师
123456789	数据结构	张瑞霞
987654321	网络渗透测试	xx
135792468	信息安全数学基础	xxx

id	username	password
1	admin	123456
2	root	root
3	admin888	888888

每一张表的每一行数据就是==数据元素==

每一行里面的列值就是==数据项==，比如课程名字、password

几行几列，行的值最大能存储多少字节，能不能为空，列的数据类型是什么，表头是什么，这些是开发设计的==数据结构==

单独的一张表就是叫==数据对象==，比如憨憨弱口令表就是一个数据对象，课程表也是一个数据对象

---

• 前驱：一个结点前面的结点叫前驱
• 后继：一个结点后面的结点叫后继

所以很明显开始的结点没有前驱，结束的结点没有后继，我当时听课还想老半天

数据的逻辑结构

就是数据元素之间的逻辑关系，常见以下四种：

• 集合：结点之间没有关系
• 线性结构：结点之间一对一联系起来，==一根绳上的蚂蚱==
• 树形结构：结点之间一对多的关系，==叫树形结构的原因也是因为和现实生活中的树的树枝很像吧==
• 图形结构：结点之间多对多的关系

数据的存储结构

• 顺序存储结构：拿计算机里一组连续的存储单元来存放数据，用内存地址来体现逻辑关系，可以理解为逻辑关系和物理位置是一样的，都排好队。对应之后学习的==顺序表==
• 链式存储结构：数据元素存放位置由编译器随机分配，数据元素之间的逻辑关系就不能通过物理位置来体现，需要用指针来把分散的结点串起来。对应之后学习的==链表==
• 索引存储结构：在存储结点的时候同时增加一个索引表，表中的每一项作为索引项，需要包含一个结点的关键码（准确识别）和存储位置
• 散列储存结构：将结点的关键字作为散列函数的输入，散列函数输出的是结点的存储位置

数据的操作

优秀的算法

算法复杂度

• 分时间复杂度和空间复杂度

时间复杂度

算法的基本操作重复执行的次数用T(n)表示，再来一个辅助函数f(n)，当 n 趋于正无穷的时候，T(n)/f(n)为一个常数，即辅助函数是执行次数的同数量级函数时，时间复杂度就是O(f(n))

分析方法

1. ==只关注循环执行次数最多的那段代码==

   ==时间复杂度是一种变化的趋势，当 n 趋于无穷大时，通常忽略掉常量、低阶和系数的影响，只记录大的高阶量==

   int f0x(int n)
   {
       int sum = 0;
       int i = 0;
       for(i = 0;i < n;i++)
       {
           sum += i;	//求和
       }
       return sum;
   }
   // 这段代码我们就只用看 sum+=1 循环了 n 次，所以时间复杂度就是O(n)

2. 加法法则

   int f0x(int m, int n)
   {
       int sum_1 = 0;
       int i = 0;
       for(i = 0;i < n;i++)
       {
           sum_1 += i;	//求和
       }
       
       int sum_2 = 0;
       i = i ^ i;	//把i置零
       for(i = 0;i < m;i++)
       {
           sum_2 += i;	//求和
       }
       return sum_1 + sum_2;
   }
   //无法评估 m 和 n 同时趋于正无穷时哪个大，所以用加法法则 T1(m)+ T2(n) = O(f(m)) + O(f(n))

3. 乘法法则

   int f0x(int n)
   {
       int flag = 0;	//计数器
       int i = 0;
       int j = 0;
       for(i = 0;i < n;i++)	//执行 n+1 次
           for(j = 0;j < n;j++)	//执行 n(n+1) 次
               flag++;	//执行 n^2次
       return flag;
   }
   //一组嵌套的 for 循环，T(n)=2n^2+2n+1，取同数量级 n^2作为时间复杂度，即O(n^2)

举例

• 线性级数O(n)

  for(flag = 0,i = 0;i < n;i++)	// n+1 次
      flag++;	//n 次
  // T(n)=2n+1

  for(flag = 0,i = 1;i <= n;i = i * 2)
      for(j = 1;j <= i;j++)
          flag++;

  第三行的执行次数是一个等比数列的和，等比数列为 1+2+4+2^(log2^n^+1)+… ，利用高等数学的知识可以知道时间复杂度为 O(n)

• 对数级数O(logx^n^)

  for(flag = 0,i = 1;i <= n;i = i * x)
      flag++;
  // 当 n=1时，循环执行1次,n=x^2时，循环执行2次，n=x^3时，循环执行3次，数学规律为循环执行logxn次
  // T(n)=logxn

• 平方级数O(n^2^)

  for(flag = 0,i = 0;i < n;i++)	// n+1 次
      for(j = 0;j < n;j++)	// n 次
          flag++;	// n(n+1)次
  // T(n)=2n^2+2n+1

• 二阶级数O(nlogx^n^)

  for(flag = 0,i =0;i < n;i++)
      for(j = 1;j <= n;j = j * x)
          flag++;
  // 第一行执行 n+1 次，第二行执行 logxn 次，第三行执行 nlogxn 次
  // T(n)= n+1+logxn+nlogxn

  • 二阶级数的内外层循环调换顺序结果也是一样

第一章结束，概念比较多，时间复杂度比较重要

去csdn看到的比较好的文章

https://blog.csdn.net/weixin_39596963/article/details/80987779?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522160099621219724835865369%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=160099621219724835865369&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v25-1-80987779.first_rank_v2_rank_v25&utm_term=%E6%B8%90%E8%BF%9B%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6&spm=1018.2118.3001.4187

https://blog.csdn.net/qq_41523096/article/details/82142747?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522160099621219724835865369%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=160099621219724835865369&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~top_click~default-3-82142747.first_rank_v2_rank_v25&utm_term=%E6%B8%90%E8%BF%9B%E6%97%B6%E9%97%B4%E5%A4%8D%E6%9D%82%E5%BA%A6&spm=1018.2118.3001.4187

---

第二章 线性表

• 线性表是由 n(n>=0) 个性质相同的数据元素组成的==有限序列==
• 同一线性表中的元素类型相同
• 主要操作有：创建空线性表、判断线性表是否为空、插入、删除和查找等基本操作

顺序表

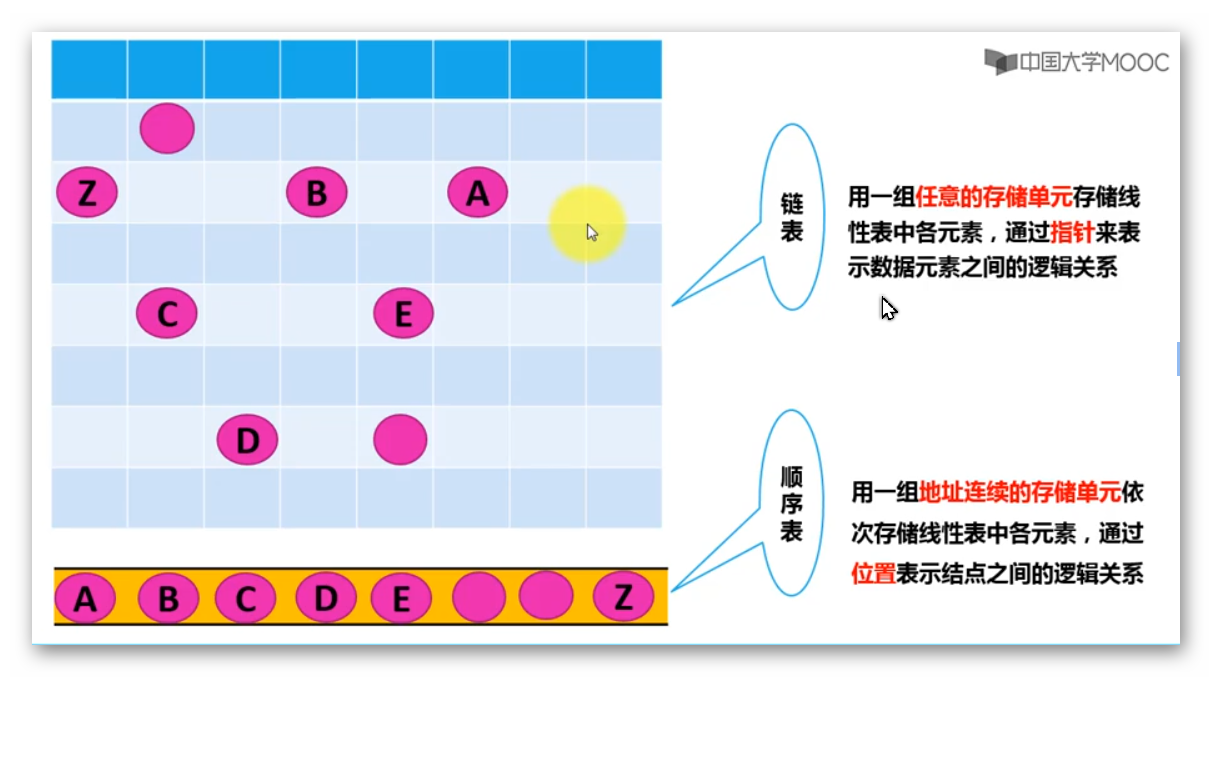
• 顺序表用一组==地址连续的存储单元==依次存储线性表中的各元素，通过位置来表示数据元素之间的逻辑关系，数据元素的逻辑关系和物理关系一样

顺序表类型定义

typedef int DataType;	//给 int 换名字
struct List	//定义顺序表类型
{
    int Max;	//最大元素个数
    int n;	//实际元素个数
    DataType *elem;	//首地址
};
typedef struct List *SeqList;	//把顺序表类型名字换成 *SeqList

顺序表建立和判空

SeqList SetNullList_Seq(int m)	//创建空顺序表，m为顺序表最大值
{
    SeqList slist = (SeqList)malloc(sizeof(struct List));	//申请结构体List空间
    if(slist != NULL)
    {
        slist->elem = (DataType*)malloc(sizeof(DataType)*m);	//申请顺序表空间，大小为m个DataType空间
        if(slist->elem)
        {
            slist->Max = m;	//顺序表最大值
        	slist->n = 0;	//顺序表长度赋值为0
            return(slist);	//返回slist首地址
        }
        else free(slist);
    }
    printf("out of space!\n");
    return NULL;
}

int IsNullList_seq(SeqList slist)	//判断顺序表是否为空
{
    return(slist->n == 0);	//顺序表长度为0则是空的，如果为空 return(1)，如果不为空 return(0)
}

顺序表插入元素

1. 移动结点
2. 插入结点
3. ==增加表长==
4. 检查表空间是否已满
5. 检查插入位置有效性
6. ==从最后一个结点开始向后移动==
7. 平均时间复杂度是 O(n)

int InsertPre_seq(SeqList slist, int p, DataType x)	//在表slist的 p 位置之前插入 x，成功返回1，否则返回0
{
    int q;
    if(slist->n >= slist->Max)	//检查表空间是否已满
    {
        printf("overflow");
        return 0;
    }
    if(p < 0 || p > slist->n)	//检查插入位置有效性
    {
        printf("not exist!");
        return 0;
    }
    for(q = slist->n - 1; q >= p; q--)	//插入位置以及之后的元素后移
    {
        slist->elem[q+1] = slist->elem[q];
    }
    slist->elem[p] = x;	//插入 x 元素
    slist->n = slist->n+1;	//表长+1
    return 1;
}

顺序表删除

1. 移动结点
2. ==减少表长==
3. 检查删除位置有效性
4. ==从删除位置的下一个元素开始移动==
5. 平均时间复杂度是O(n)

int Delindex_seq(SeqList slist,int p)	//删除下标为 p 的元素
{
    int q;
    if(p < 0 || p >= slist->n)	//检查删除位置有效性
    {
        printf("Not exist\n");
        return 0;
    }
    for(q = p; q < slist->n-1; q++)	//p位置之后的元素向前移动
    {
        slist->elem[q] = slist->elem[q+1];
        slist->n = slist->n-1;	//表长-1
        return 1;
    }
}

这里老师出了一个思考题，如何删除顺序表中所有值为 x 的元素

思路：把不等于 x 的元素提出来重新放到一个新数组里，建立flag变量来记录表长

void deleteX_seq(SeqList slist,int x)
{
    int i = 0;	//循环变量
    int flag = 0;	//循环变量
    for(i = 0;i < slist->n; i++)	//遍历顺序表
    {
        if(slist->elem[i] != x)
        {
            slist->elem[flag] = slist->elem[i];	//把值不是 x 的元素放到新数组里
            flag++;	//用来记录新的表长
        }
    }
    slist->n = flag;	//更新新表长
}

顺序表查找定位

int LocateIndex_seq(SeqList slist, int x)	//遍历顺序表查找值为x的元素，返回其下标
{
    int i = 0;	//循环变量
    for(i = 0;i < slist->n;i++)
    {
        if(slist->elem[i] == x)
        {
            return i;
        }
    }
    return -1;	//查找失败返回-1
}

已经排好序的顺序表可以采用二分法查找，详见书P28页

单链表

• 链表用一组==任意的存储单元==存储线性表中各元素，通过指针来表示数据元素之间的逻辑关系，数据元素的逻辑关系和物理关系不一样
• ==单链表的一个重要特性就是只能通过前驱结点找到后续结点，而无法从后续结点找到前驱结点==

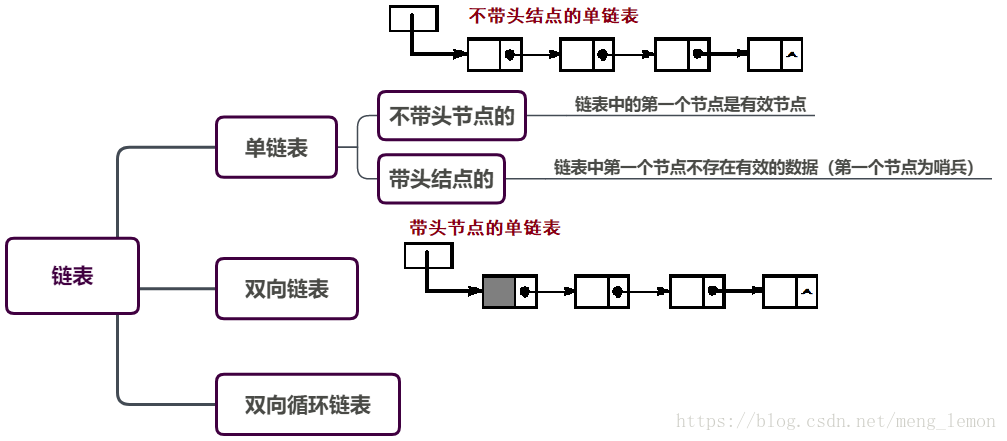
建立	插入	删除	查找	输出
头插法	前插法	删除 P 后继	序号查找	顺序打印
尾插法	后插法	删除 P 本身	值查找
递归法		按值删除

链表类型定义

typedef int DataType;
struct Node
{
    DataType data;		//数据域
    struct Node *next;	//指针域
};
typedef struct Node *PNode;		//结点类型重命名
typedef struct Node *LinkList;	//单链表类型重命名，方便区分

指针域为什么要定义成 struct Node *类型？

这个问题想了我二十分钟T_T，原来就是因为指针域的指针要指向下一个结点，下一个结点的数据类型就是struct Node类型，麻了，又是简单的问题想老半天

单链表建立和判空

• 建立带有头结点的空的单链表，为了方便后面的算法运算

LinkList SetNullList_Link()	//创一个带有哨兵的空链表
{
    LinkList head = (LinkList)malloc(sizeof(struct Node));	//申请头结点空间
    if(head != NULL)
    {
        head->next =NULL;	//头结点的指针域赋值为NULL
    }
    else
    {
        printf("Alloc failure");
    }
    return head;	//返回头结点的地址
}

int IsNull_Link(LinkList head)	//判空函数，如果为空返回1，不为空返回0
{
    return(head->next == NULL);
}

头插法建立非空单链表

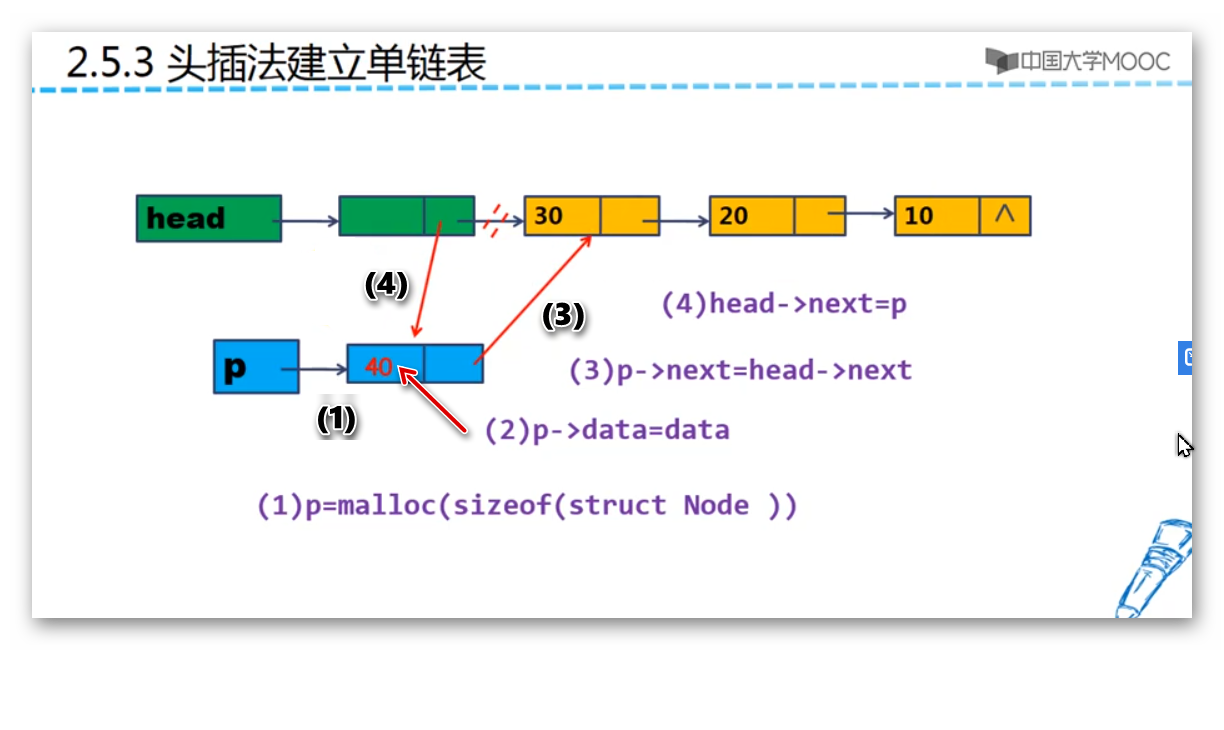
第三步和第四步不能够颠倒顺序，如果先做第四步，那么头结点会和后面的结点断开联系

void CreateList_Head(struct Node *head)	//头插法建立非空单链表
{
    PNode p = NULL;	//建立空结点
    int data;
    printf("请输入整型数据建立链表，以-1结束\n");
    scanf_s("%d", &data);	//输入数据域内的值
    while(data != -1)
    {
        p = (struct Node*)malloc(sizeof(struct Node));	//为空结点申请内存
        p->data = data;	//数据域赋值
        p->next = head->next;	//头结点指针域赋值给插入节点的指针域
        head->next = p;	//新插入结点地址赋值给head->next
        scanf_s("%d", &data);	//输入下一个数据结点的数据域
    }
}

尾插法建立单链表

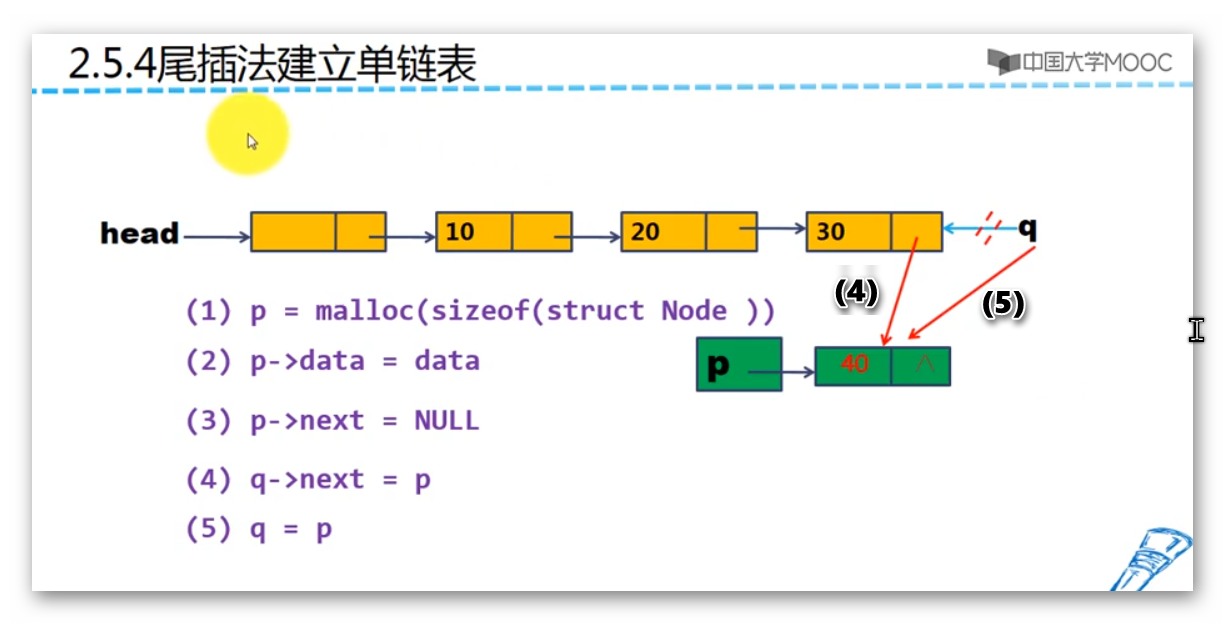
同样的第四步和第五步不能调换顺序，如果先做第五步，尾指针就会失去和尾结点的联系，就没办法再进行第四步了

void CreateList_Tail(struct Node *head)	//尾插法建立非空单链表
{
    struct Node *p = NULL;
    struct Node *q = head;
    int data;
    printf("请输入整型数据建立链表，以-1结束\n");
    scanf_s("%d", &data);
    while(data != -1)
    {
        p = (struct Node*)malloc(sizeof(struct Node));	//为空结点申请内存
        p->data = data;	//新结点数据域赋值
        p->next = NULL;	//插入结点指针域赋值为NULL
        q->next = p;	//最后一个结点指针域指向新插入结点
        q = p;	//最后一个结点地址赋值给尾指针
        scanf_s("%d", &data);
    }
}

单链表查找

按值查找

找数据域值为给定值x的结点，找到的话，返回其第一次出现的存储位置，否则返回NULL

PNode Locate_Link(LinkList llist, DataType x)	//传进去llist链表，查找值为x的元素
{
    PNode p;	//用于遍历链表的指针
    if(llist == NULL)
        return NULL;
    p = llist->next;	//p指针指向第一个有效结点
    while(p != NULL&&p->data != x)	//当 p = NULL时或 p->data=x时，退出循环，否则指针指向下一个结点
        p = p->next;
    return p;
}

按照序号查找

找链表中第i个结点，找到的话，返回该结点的存储位置，否则返回NULL

PNode Locate_Link2(Linklist llist,int x)
{
    PNode p;
    int flag;
    if(llist == NULL)
        return NULL;
    p = llist->next;
    while(p!=NULL&&flag!=x)
    {
        p=p->next;
    }
    return p;
}

单链表插入

后插法

//在链表llist中的p位置之后插入值为x的结点
int InsertPost_link(LinkList llist,PNode p,DataType x)
{
    PNode q;
    if(p == NULL)
    {
        printf("data don't exist");
        return 0;
    }
    q = (PNode)malloc(sizeof(struct Node));
    if(q != NULL)
    {
        q->data = x;
        q->next = p->next;
        p->next = q;
        return 1;
    }
    else
    {
        printf("malloc 失败\n");
        return 0;
    }
}

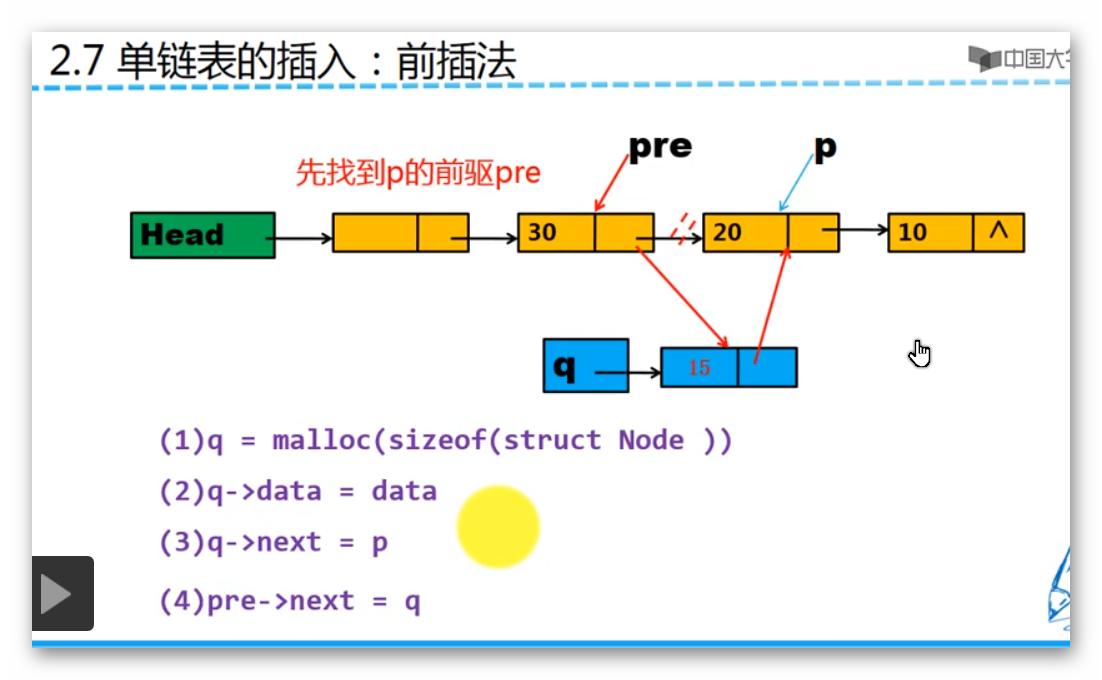
前插法

前插法首先要找到p的前驱结点pre，然后转化为后插法来插入

int InsertPre_link(LinkList llist.PNode p,DataType x)
{
    Pnode prt = llist;
    PNode q = NULL;
    while(pre->next != p)	
    {
        pre = pre->next;
    }
    q = (PNode)malloc(sizeof(struct Node));
    if(	q ==NULL)
        return 0;
    q->data = x;
    q->next = p;
    pre->next = q;
    return 1;
}

单链表删除

删除结点的后继

void DelPostionNext_Link(LinkList head,PNode r)
{
    if(r->next)
    {
        PNode p = r->next;
    	r->next = p->next;
    	free(p);
    }
}

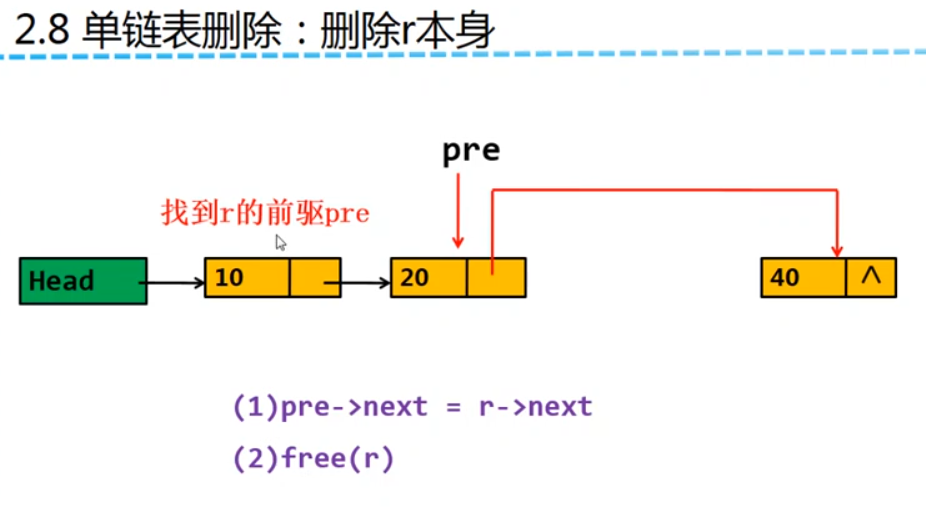
删除结点本身

删除结点本身需要先找到结点的前驱，然后转化为删除结点的后继来做

void DelPostion_Link(LinkList head,PNode r)
{
	PNode  pre = head; 
	while(pre->next != r)
    {
        pre = pre->next;
    }
    pre->next = r->next;
    free(r);
}

按值删除

按值删除的原理就是用两个指针一前一后遍历链表，后面的指针找到要删除结点之后把指针域赋值给前一个指针的指针域，然后自我释放，原理等同于删除自身结点的算法

//删除第一个与输入参数data相等的值的结点
void DelValue_Link(LinkList head,int data)
{
    PNode p = head->next;
    PNode before_p = head;
    while(p != NULL)
    {
        if(p->data == data)
        {
            before_p->next = p->next;
            free(p);
        }
        else
        {
            p = p->next;
            before_p = before_p->next;
        }
    }
}

单链表逆置

这是在课堂上当堂练习的内容，记录下来，直接贴算法吧

void Reverse(LinkList H)
{
    PNode a,b;
    a = H->next;    //用一个指针记录下第一个结点
    H->next = NULL; //头结点指针域置空，把头结点独出来
    while(a)        //进入循环，循环到最后一个结点为NULL时结束循环
    {
        b = a;                  //用另一个指针记录下后继结点
        a = a->next;            //移动到下一个结点
        b->next = H->next;      //头结点指针域指向分离出来的那个结点
        H->next = b;            //不懂怎么表达这句话的意思
    }
}

单循环链表和双循环链表记得更新

已更新

单循环链表

为了解决知道链表中某个结点的位置而无法找到其前驱的问题，引入了循环链表，就是让最后一个结点指向头结点

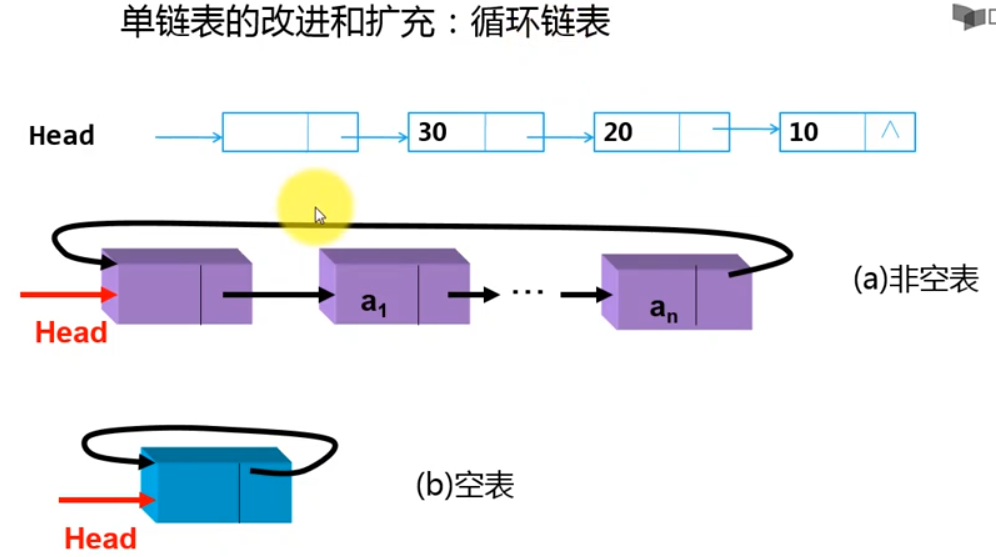
为了方便利用，多采用尾指针rear来表示单循环链表，头结点则表示为rear->next，第一个结点则表示为rear->next->next

//建立尾指针表示的单循环链表
typedef int DataType;
struct Node;
typedef struct Node *PNode;
struct Node{
    DataType data;
    PNode next;
};
typedef struct Node *CLinkList;
CLinkList createListRearCircle()
{
    PNode rear;
    Pnode s;
    int x;
    CLinkList head = (CLinkList)malloc(sizeof(CLinkList));
    head->next = head;
    rear = head;
    printf("请输入整型数据建立链表，以-1结束\n");
    scanf_s("%d"&x);
    whlie(x!=-1)
    {
        s = (PNode)malloc(sizeof(CLinkList));
        s->data = x;
        s->next = head;
        rear->next = s;
        rear = s;
        scanf_s("%d",&x);
    }
    return rear;
}

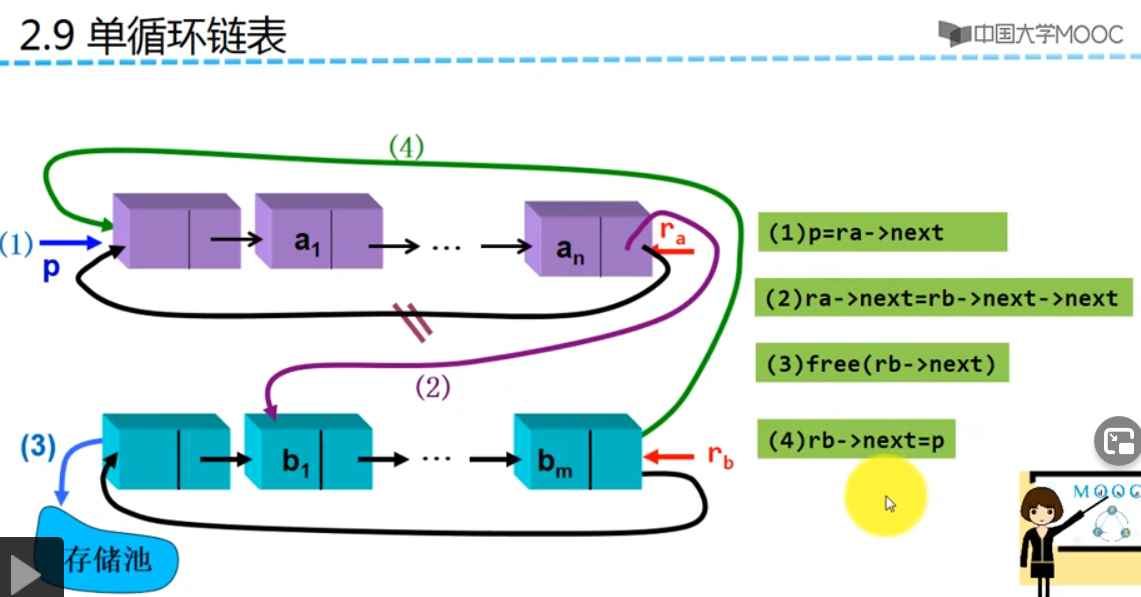
两个单循环链表合并成一个新的单循环链表

CLinkList Combine(CLinkList a,CLinkList b)
{
    PNode p = a->next;
    a->next = b->next->next;
    free(b->next);
    b->next = p;
    return b;
}

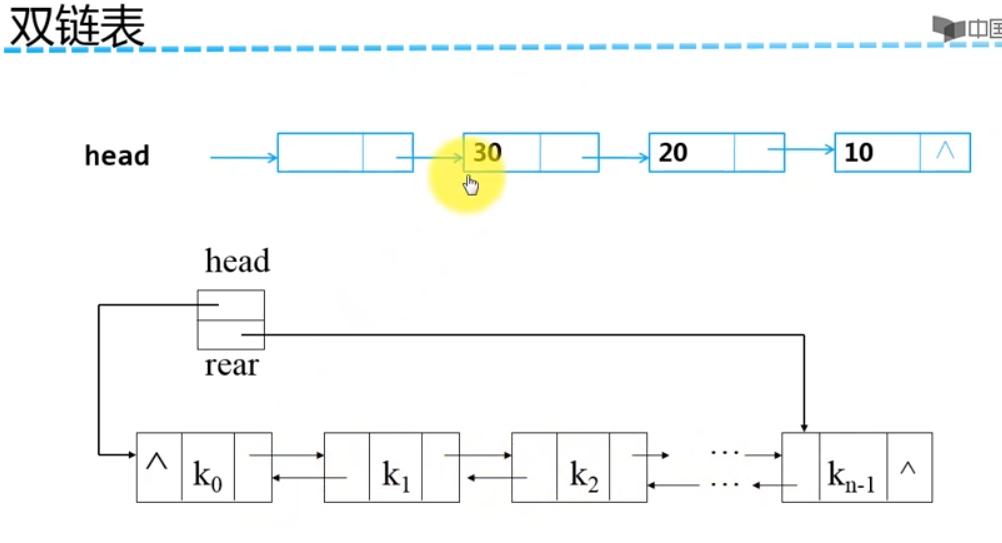
双链表和双循环链表

双链表

//类型定义
typedef struct node		//双链表结点类型
{
    DataType data;
    struct node *llink;	//前驱指针
    struct node *rlink;	//后继指针
}Dlnode;
typedef					//头尾结点指针类型（head）
{
    DLnode *first;
    DLnode *last;
}DLinkList;
DLinkList *dlist;

双链表删除

void Del_DoubleList(DLinkList dlist,Dlnode *p)
{
    p->llink->rlink = p->rlink;
    p->rlink->llink = p->llink;
}

双链表插入

void Insert_DoubleList(Dlnode *p)
{
    Dlnode s = (Dlnode)malloc(sizeof(Dlnode));
    if(s)
    {
        s->llink = p;
        s->rlink = p->rlink;
        p->rlink->llink = s;
        p->rlink = s;
    }
    else
    {
        printf("malloc失败\n");
        exit(0);
    }
}

双循环链表

把双链表最后一个结点的后继指针指向第一个结点，把第一个结点的前驱指针指向最后一个结点，就组成了双循环链表

第三章 栈和队列

• 栈和队列其实是线性表的特例，特殊性在于它们都是操作受限的线性表

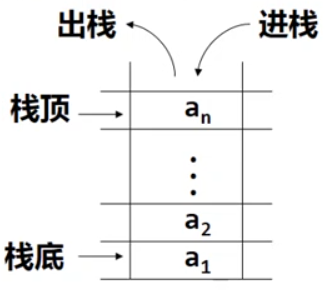
栈

• 栈限定在表尾进行插入或删除，表尾端称栈顶，表头端称栈底
• 后进先出

栈混洗

• n个数据以此进栈，随时可能出栈，按照出栈顺序得到的一个序列，称为一个栈混洗
• 任一前缀中的 push 不少于 pop ，则该序列也必然对应一个栈混洗

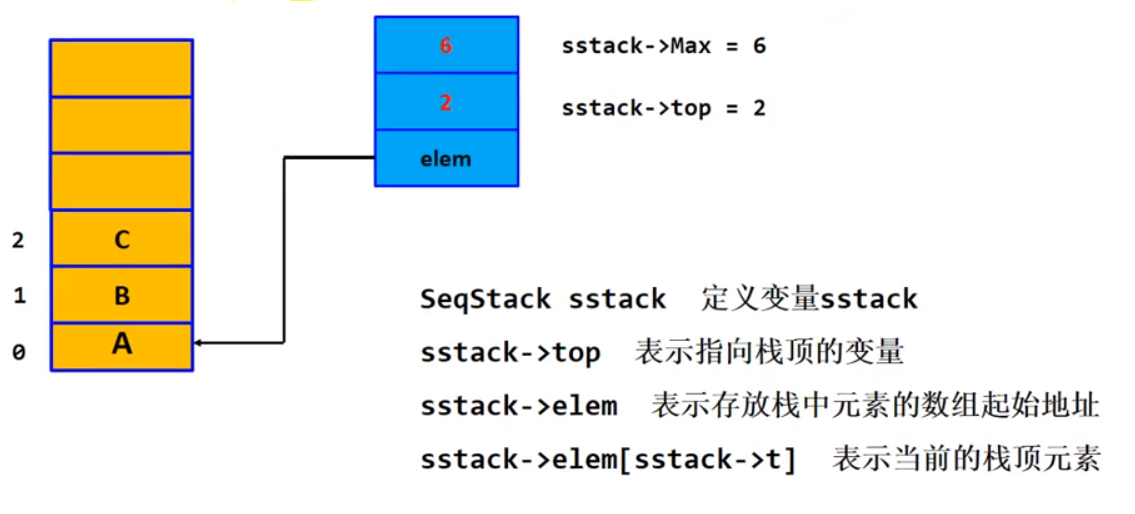
顺序栈

• 静态结构，需提前分配存储空间
• 注意判断栈满或栈空

顺序栈类型定义

typedef int DataType;
struct Stack
{
    int MAX;	//最大容量
    int top;	//栈顶指针
    DataType *elem;	//存放元素的数组的起始指针
};
typedef struct Stack *SeqStack	//定义顺序栈类型

创建空栈

SeqStack SetNullStack_Seq(int m)	//创建空顺序栈，m 为分配的最大空间
{
    SeqStack sstack = (SeqStack)malloc(sizeof(struct Stack));
    if(sstack != NULL)
    {
        sstack->elem = (int*)malloc(sizeof(int) * m);
        if(sstack->elem != NULL)
        {
            sstack->MAX = m;		//顺序栈最大容量
            sstack->top = -1;		//设置栈顶初值为1
            return(sstack);
        }
        else
        {
            free(sstack);
            return NULL;
        }
    }
    else
    {
        pritnf("Alloc failure!");
        return NULL;
    }
}

顺序栈判空

int IsNullStack_seq(SeqStack sstack)		//判空函数
{
    return(sstack->top == -1);		//栈顶元素 top 用来判断，如果为空返回 1 ，如果不为空返回 0 
}

进栈

• 需要检查栈是否已满

void Push_seq(SeqStack sstack, int x)		//入栈
{
    if(sstack->top >= (sstack->MAX - 1))	//检查栈满函数
    {
        printf("栈满了，再加栈溢出了!");
    }
    else
    {
        sstack->top ++;		//修改栈顶变量
        sstack->elem[sstack->top] = x;		//把元素放进栈顶变量的位置中
    }
}

sstack->top用来表示数组下标

必须先修改栈顶指针，sstack->top++，然后再把元素放进去

出栈

• 需要检查栈是否已空

void Pop_seq(SeqStack sstack)		//出栈
{
    if(IsNullStack_seq(sstack))		//调用判断栈空函数
        printf("栈空了!");
    else
    {
        sstack-top = sstack-top - 1;//栈顶-1
    }
}

取栈顶元素

• 需要检查栈是否已空

DataType Top_seq(SeqStack sstack)		//取栈顶元素的值
{
    if(IsNullStack_seq(sstack))		//调用判断栈空函数
        printf("栈空了!");
    else
    {
        return sstack-> elem[sstack->top];
    }
}

链栈

• 用链式存储的栈， top 指向栈顶元素，栈底在链表尾部
• 指针从栈顶开始，往栈底方向链接，有头结点
• 

链栈类型定义

typedef int DataType;
struct Node
{
    DataType data;
    struct Node* next;
};
typedef struct Node *PNode;					//结点类型
typedet struct Node *top, *LinkStack;		//栈顶和链栈类型

创建空栈

LinkStack SetNullStack_Link()		//创建空链栈
{
    LinkStack top = (LinkStack)malloc(sizeof(struct Node));
    if(top != NULL)
        top->next = NULL;			//头结点指针域置空
    else
        printf("Alloc failure");
    return top;						//返回栈顶指针
}

判断栈空

• 判断栈顶结点的指针域是否为NULL，空则返回1，否则返回0

int IsNullStack_link(LinkStack top)		//判断链栈是否为空
{
    if(top->next == NULL)
        return 1;	//为空返回1
    else
        return 0;	//不为空返回0
}

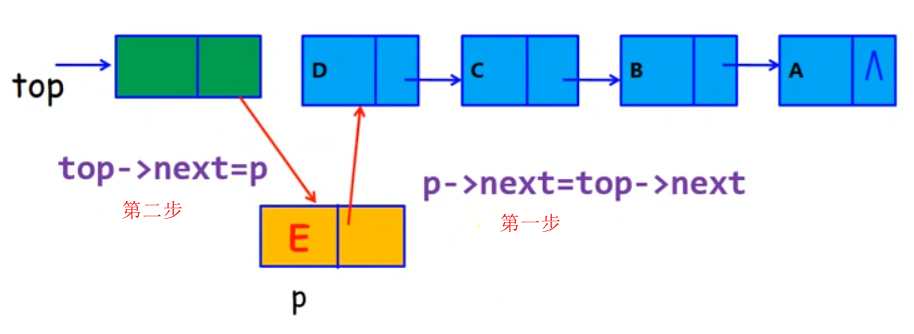
进栈

• 进栈操作的关键点和链表的关键点一样：==只能是前驱找后继，后继找不到前驱==，所以进栈的指针指向顺序有讲究
  1. 头结点指针域赋值给要插入元素指针域
  2. 头结点指针域指向要插入元素
• 栈的插入操作只能是在栈顶，即在头结点处进行进栈操作

void Push_link(LinkStack top, DataType x);			//进栈
{
    PNode p;
    p = (PNode)malloc(sizeof(struct Node));			//申请结点空间
    if(p == NULL)
        printf("Alloc failure");
    else
    {
        p->data = x;								//数据域赋值
        p->next = top->next;						//指针域赋值
        top->next = p; 								//修改栈顶
    }
}

出栈

• 出栈需要判空，需要释放结点空间

void Pop_link(LinkStack top)		//删除栈顶元素
{
    PNode p;
    if(IsNullStack_link(top))		//判断栈空
        printf("是空的");
    else
    {
        p = top->next;				//p 指向待删除结点
        top->next = p->next;		//修改栈顶指针
        free(p);					//释放删除结点空间
    }
}

取栈顶元素

• 需要判空

DataType Top_link(LinkStack top)	//删除栈顶元素
{
    if(IsNullStack_link(top))		//判断栈空
        printf("是空的");
    else
    {
        return top->next->data;		//头结点指针域指向的就是栈顶的结点
    }
}

这里以后有空要记得补上栈的应用的一些代码

栈实现：进制转换

转八进制

void Conversion(LinkStack ps, int n)	//十进制转八进制
{
    int temp;
    while(n)
    {
        Push_link(ps,n%8);
        n/=8;
    }
    printf("结果为:");
    while(!IsNullStack_Link(ps))
    {
        temp = Top_link(ps);
        printf("%d",temp);
        Pop_link(ps);
    }
}

转十六进制

void Hexconversion(LinkStack ps,int n)
{
    int temp;
    while(n)
    {
        int temp = n%16;
        switch(temp)
        {
            case 10:temp = 'A';break;
            case 11:temp = 'B';break;
            case 12:temp = 'C';break;
            case 13:temp = 'D';break;
            case 14:temp = 'E';break;
            case 15:temp = 'F';break;
        }
        Push_link(ps,temp);
        n/=16;
    }
    printf("结果为:");
    while(!IsNullStack_Link(ps))
    {
        temp = Top_link(ps);
        if(temp<10)
            printf("%d",temp);
        else
        	printf("%c",temp);
        Pop_link(ps);
    }
}

栈实现：括号匹配

• 算法思路

  • 所有的左括号都进栈，设置标志位flag为1

  • 遇到右括号开始匹配，首先检查栈是否为空

    • 如果栈空，表示匹配失败，右括号多了

    • 如果栈不空

      • 如果匹配到左括号，左括号出栈

      • 如果不匹配，flag设为0

  • 检验结束时

    • 栈不为空或者flag为0，则表示匹配不成功
    • 栈空，则表示匹配成功

int BracketMatch(LinkStack top)
{
    int flag = 1;
   	char ch,temp;
    Push_link(top,'#');	//栈底放#，结束标志位
    printf("输入要判断表达式，用#表示结束：\n");
    scanf_s("%c",&ch);
    while(ch!='#')
    {
        if(ch = '(')
        {
            Push_link(top,ch);
        }
        else
        {
            if(ch = ')'&&!IsNullStack_Link(top))
            {
                temp = Top_link(top);
                if(temp == '(')
                {
                    Pop_link(top);
                }
                else
                {
                    flag = 0;
                    break;
                }
            }
        }
        scanf_s("%c",&ch);
    }
    if(!flag||Top_link(top)!='#')
    {
        printf("no\n");
        return 0;
    }
    else
    {
        printf("yes\n");
        return 1;
    }
}

队列

• 队列限定在一端进行插入、一端进行删除，插入端称队尾，删除端称队头
• 先进先出

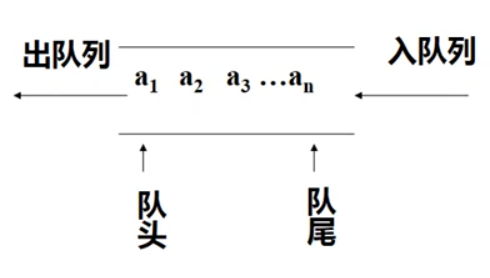
队列会存在假溢出的情况，即当前队列并不满，但是不能入队

原因：被删除的元素的空间没有再被使用

解决：循环队列

循环队列

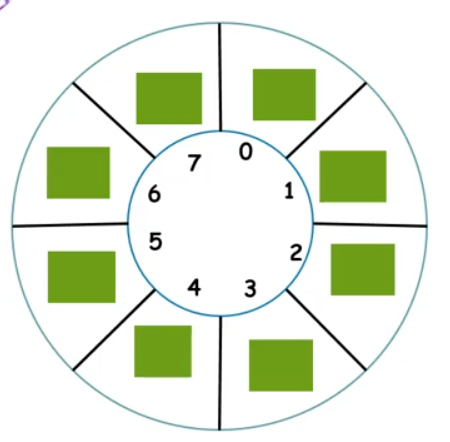
循环队列类型定义

typedef int DataType;
struct Queue
{
    int Max;		//队列空间最大值
    int f,r;		//队头指针和队尾指针
    DataType *elem;	//队列元素空间
};
typedef struct Queue *SeqQueue;

创建空队列

SeqQueue SetNullQueue_Seq(int m)
{
    SeqQueue squeue;
    squeue = (SeqQueue)malloc(sizeof(SeqQueue));
    if(squeue == NULL)
    {
        printf("malloc失败\n");
        return NULL;
    }
    else
    {
        squeue-elem = (int *)malloc(sizeof(DataType)*m);
        squeue->Max = m;
        squeue->f = 0;
        squeue->r = 0;
        return squeue;
    }
}

判断队空

• 检查队头和队尾指针是否相等，如果相等为空队列，返回1，否则返回0

int IsNullQueue_seq(SeqQueue Squeue)
{
    return (squeue->f == squeue->r);
}

入队

• 若队列没满，在队尾添加元素，修改队尾指针

void EnQueue_seq(Sequeue Squeue, DataType x)
{
    if((squeue->r+1)%squeue->Max == squeue->f)
        printf("队列已满\n");
    else
    {
        squeue->elem[squeue->r] = x;				//插入元素x
        squeue->r = (squeue->r+1) % (squeue->Max);	//队尾指针++
    }
}

出队

• 首先判断队列是否为空，非空则删除队头元素，修改队头指针

void DeQueue_seq(SeqQueue squeue)
{
    if(IsNullQueue_seq(squeue))
        printf("队列是空的\n");
    else
        squeue-f = (squeue->f+1)%(squeue->Max);
}

取队头元素

• 首先判断队列是否为空，非空则返回队头元素

DataType FrontQueue_seq(SeqQueue squeue)
{
    if(squeue->f == squeue->r)
        printf("队列是空的\n");
    else
        return squeue->elem[squeue->f];
}

链队列

链队列类型定义

typedef int DataType;
struct Node
{
    DataType data;
    struct Node *link;
};
typedef struct Node *PNode;
struct Queue
{
    PNode f;	//队头指针
   	PNode r;	//队尾指针
};
typedef struct Queue *LinkQueue;

创建空队列

LinkQueue SetNullQueue_Link()
{
    LinkQueue lqueue;
    lqueue = (LinkQueue)malloc(sizeof(LinkQueue));
    if(lqueue!=NULL)
    {
        lqueue->f = NULL;
        lqueue->r = NULL;
    }
    else
        printf("malloc失败\n");
    return lqueue;
}

判断队空

• 检查队头指针，如果为空，返回1，否则返回0

int IsNullQueue_Link(LinkQueue lqueue)
{
    return(lqueue->f == NULL);
}

入队

• 申请结点，数据域指针域赋值
  • 如果是第一个结点，特殊处理，队头和队尾指针都指向该结点
  • 如果不是第一个结点，则在队尾插入，修改队尾指针

void EnQueue_link(LinkQueue lqueue,DataType x)
{
    PNode p;
    p = (PNode)malloc(sizeof(PNode));
    if(p == NULL)
        printf("malloc失败\n");
    else
    {
        p->data = x;
        p->link =NULL;
        if(lqueue->f == lqueue->r)
        {
            lqueue->f = p;
            lqueue->r = p;
        }
        else
        {
            lqueue->r->link = p;
            lqueue->r = p;
        }
    }
}

出队

• 首先判断队列是否为空，非空则修改队头指针并释放队头结点空间

void DeQueue_link(LinkQueue lqueue)
{
    PNode p;
    if(IsNullQueue_Link)
        printf("队列为空\n");
    else
    {
        p = lqueue->f;
        lqueue->f = lqueue->f->link;
        free(p);
    }
}

取队头元素

• 首先判断队列是否为空，非空返回队头元素

DataType FrontQueue_link(LinkQueue lqueue)
{
    if(IsNullQueue_Link)
    {
        printf("队列为空\n");
    	return 0;
    }
    else
        return lqueue->f->data;
}

双端队列

同时具备栈和队列的性质的数据结构，既可以在头部和尾部插入和删除元素的数据结构

具体的东西以后学了再补上来

第四章 树与二叉树

二叉树

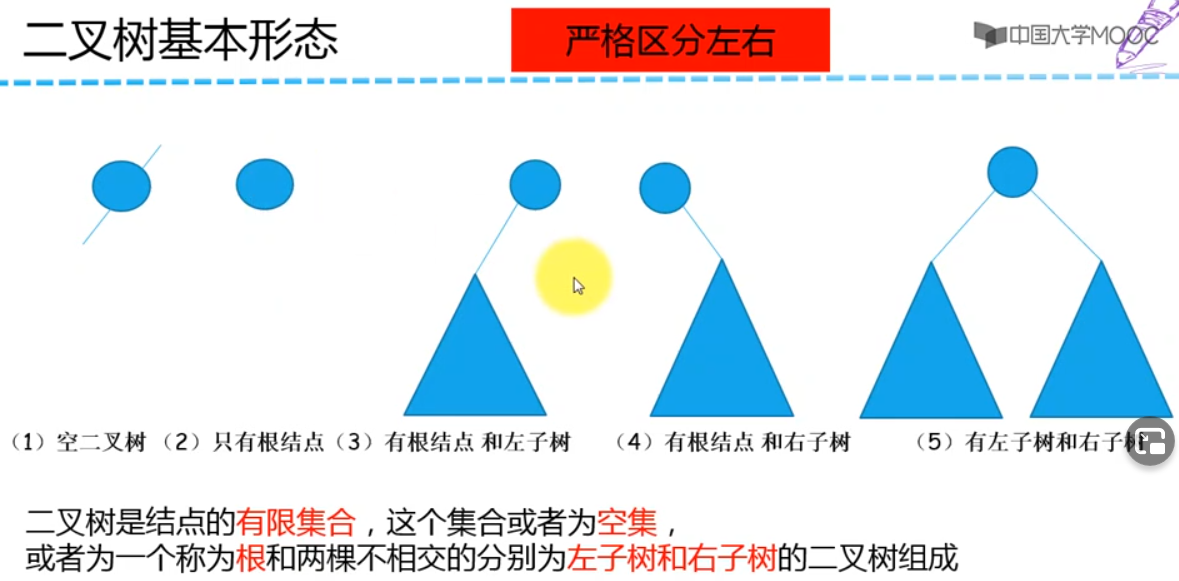
• 二叉树是结点的有限集合
• 这个集合可以是空集，也可以是一个称为根和两棵不相交的分别为左子树和右子树的二叉树组成

二叉树基本术语

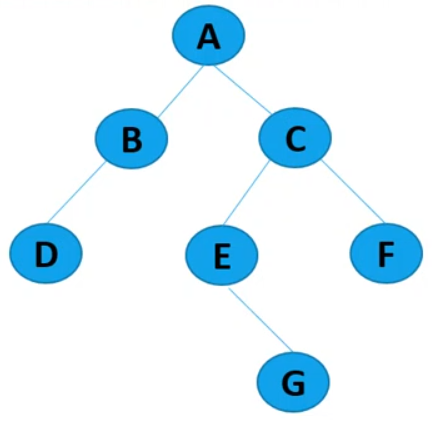
• 祖先：最早的根节点，A就是整个二叉树的祖先

  父结点：A就是B和C的父结点，B是D的父结点

  子结点：B和C就是A的子结点

• 兄弟结点：处在同一父母结点的结点，互称兄弟结点，B和C就是兄弟结点

• 结点的度：结点的孩子的个数，A的度为2

• 树叶和分支结点：度为0的叫树叶，其他都叫分支结点

• 路径：连接的边

  路径长度：层数

• 结点的层数（约定根结点为0）：B、C的层数就是1，D、E和F的层数就是2

• 二叉树的高度：二叉树当中最大的层数，就是高度，G的层数是3，高度为3

• B：分支

特殊的二叉树

满二叉树

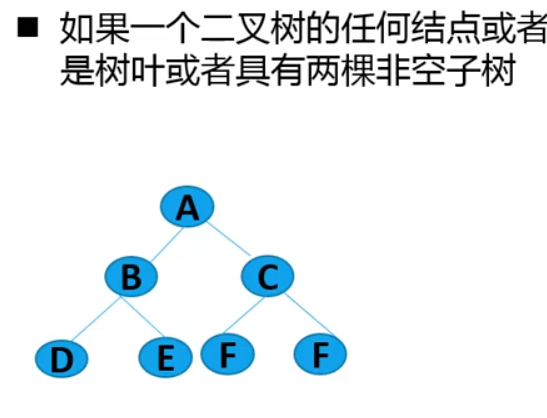
完全二叉树

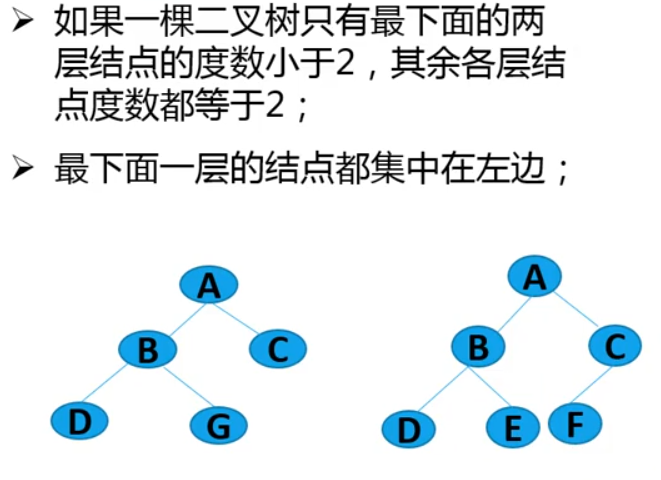
扩充二叉树

二叉树的性质

• 在非空二叉树的第==i==层上至多有==2^j^==个结点(==i>=0==)

  归纳证明：==i = 0==，==结点数=1=2^0^==，假设对于==j(0<=j<=i)==，结点数至多有==2^j^==，对于==i=j+1==，结点数至多有==2*2^j^=2^j+1^==

• 深度为 ==k==的二叉树至多有==2^k+1^-1==个结点(==k>=0==)

• 对任何一棵非空二叉树T，如果叶结点个数为==n0==，度为2的结点数位==n2==，则==n0=n2+1==

二叉树的遍历

• 沿某条搜索路径访问二叉树，对二叉树中的每个结点访问一次且仅访问一次
• 遍历一棵非空二叉树
  • 访问根节点 D
  • 遍历左子树 L
  • 遍历右子树 R

二叉树的深度遍历

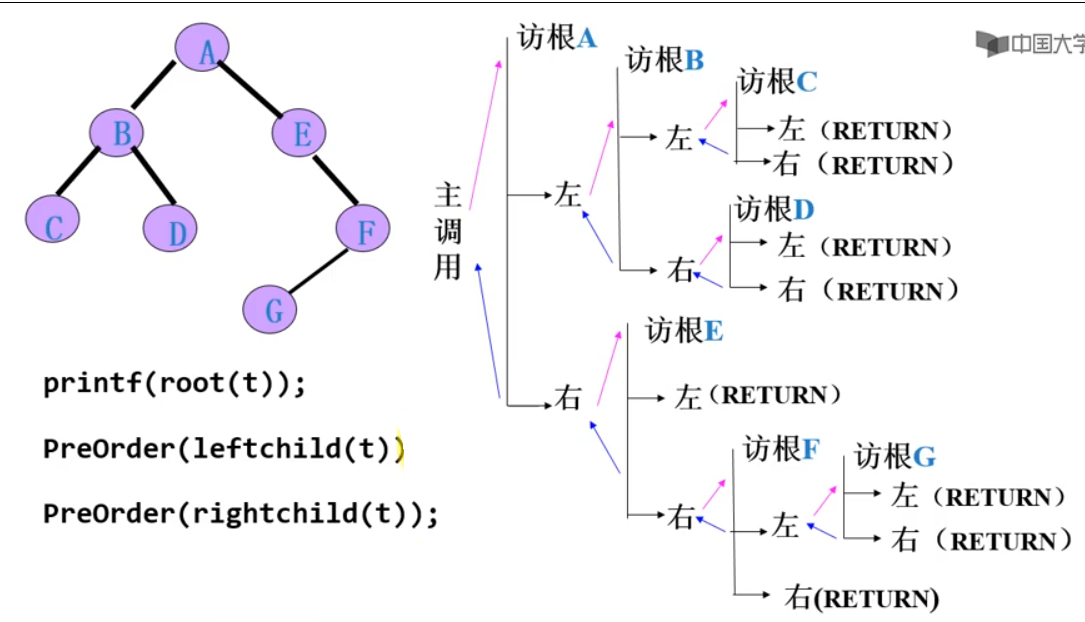
先序遍历

• 按照D->L->R的顺序访问结点
  1. 访问根节点
  2. 先根次序遍历D的左子树
  3. 先根次序遍历D的右子树
• 伪代码

void PreOrder(BinTree bt)
{
    if(bt==NULL)					//结束递归的条件
        return;					
    Visit(root(bt));				//访问结点的数据域
    PreOrder(leftchild(bt));		//先根递归遍历t的左子树
    PreOrder(rightchild(bt));	//先根递归遍历t的右子树
}

中序遍历

• 按照L->D->R的顺序访问结点
  1. 对称次序遍历左子树
  2. 访问根结点
  3. 对称次序遍历右子树
• 伪代码

void InOrder(BinTree bt)
{
    if(bt==NULL)				//结束递归的条件
        return;
    InOrder(leftchild(bt));	//对称递归遍历t的左子树
    Visit(root(bt));			//访问结点的数据域
    InOrder(rightchild(bt));	//对称递归遍历t的右子树
}

后序遍历

• 按照L->R->D的顺序访问结点
  1. 后根次序遍历左子树
  2. 后根次序遍历右子树
  3. 访问根节点
• 伪代码

void PostOrder(BinTree bt);
{
    if(bt==NULL)					//结束递归的条件
        return;
    PostOrder(leftchild(bt));	//后根递归遍历t的左子树
    PostOrder(rightchild(bt));	//后根递归遍历t的右子树
    Visit(root(bt));				//访问结点的数据域
}

---

举例：

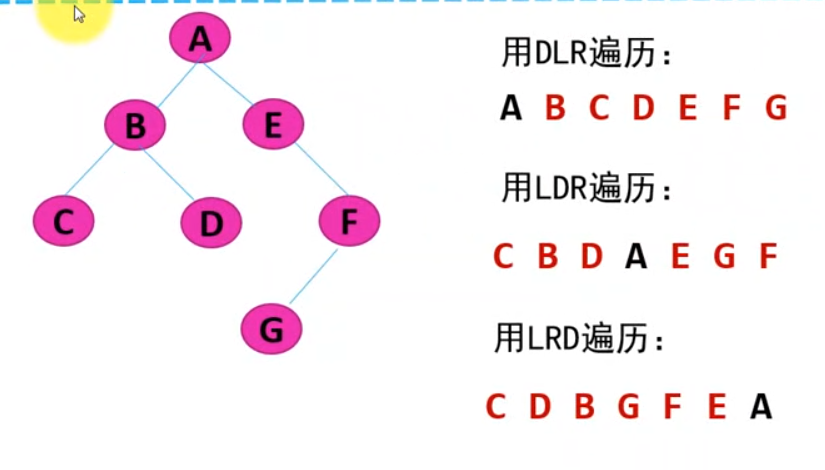
二叉树的广度遍历（层次遍历）

• 从二叉树的第一层开始，==从上到下逐层遍历，在同一层中，从左到右逐个遍历==
• 伪代码

void LevelOrder(BinTree(bt))
{
    初始化队列 q;
    if(bt==NULL)
        return;
    while(队列不空)
    {
        出队元素 p;
        visit(p);				//访问队头结点的数据域
        if(leftchild(p)!=NULL)	//队头左孩子不为空则让左孩子入队
            leftchild(p) 入队q;
        if(rightchild(p)!=NULL)	//队头右孩子不为空则让右孩子入队
            rightchild(p) 入队q;
    }
}

二叉树的交叉遍历

void PreOrder(BinTree bt)
{
    if(bt==NULL)
        return;
    visit(bt);
    InOrder(lefchild(bt));
    InOrder(rightchild(bt));
}
void InOrder(BinTree bt))
{
    if(bt==NULL)
        return;
    PreOrder(leftchild(bt));
    visit(bt);
    PreOrder(rightchild(bt));
}
void main()
{
    bt = CreateBinTree();
    PreOrder(bt);
}

二叉树的重构

• 由遍历序列恢复二叉树

==已知先根序列和对称序列可以恢复二叉树==

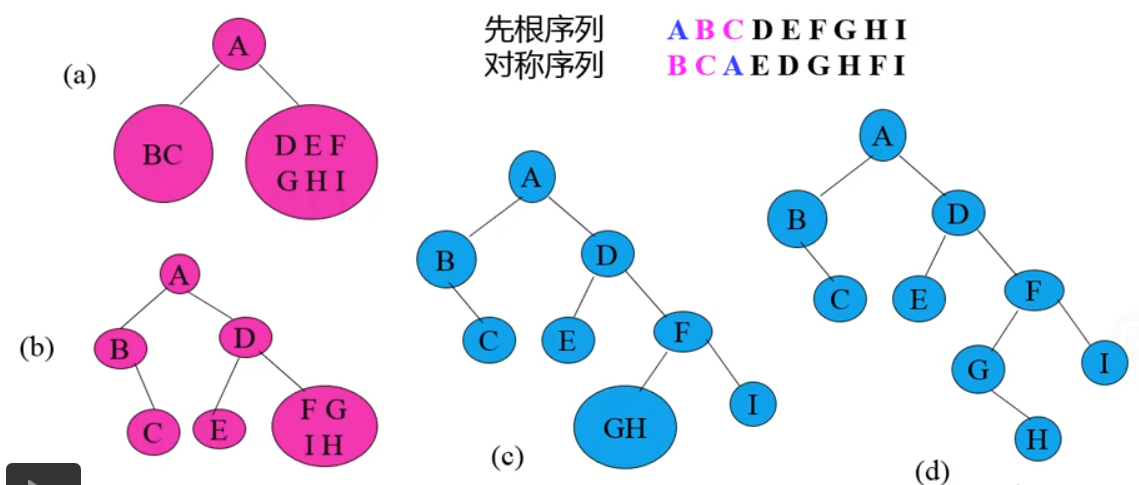
==已知对称序列和后根序列也可以恢复二叉树==

==已知先根序列和后根序列对于满二叉树可以恢复，其他不行==

因为满二叉树每个结点都有左孩子和右孩子

• 先根序列找左孩子
• 后跟序列找右孩子

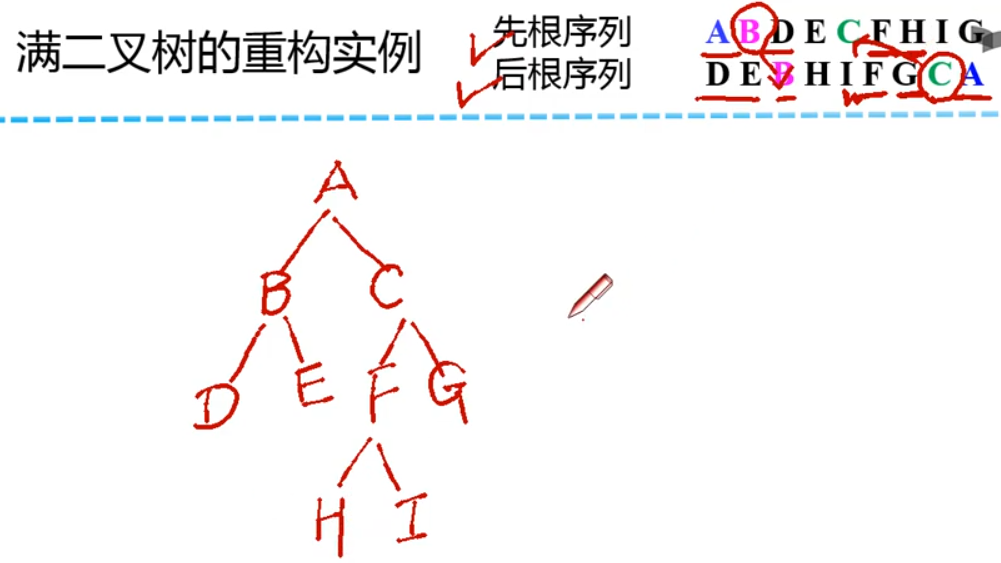
a

二叉树的存储

二叉树的顺序存储（完全二叉树）

• 用一组地址连续的存储单元按层次次序依次存储的结点

二叉树的链式存储（一般二叉树）

二叉链表：

二叉链表中，无法通过结点直接找到其双亲

解决办法是在结点中增加一个父结点指针域，转化为三叉链表

类型定义：

typedef char DataType;
typedef struct BTreeNode
{
    DataType data;
    struct BTeeNode *leftchild;
    structBTreeNode *rightchild;
}BinTreeNode;
typedef BinTreeNode *BinTree;

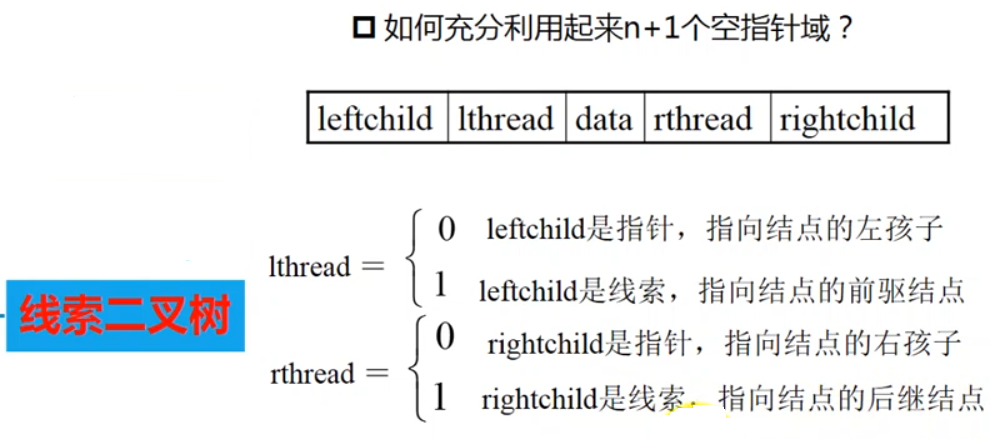
线索二叉树

• 类型定义

typedef char DataType;
typedef struct BTreeNode
{
    DataType data;
    struct BTreeNode *leftchild;
    struct BTreeNode *rightchild;
    int lthread;
    int rthread;
}BinTreeNode;
typedef BinTreeNode *BinTree;

（递归）二叉树的建立与遍历

• 建立：

BinTree CreateBinTree_Recursion()
{
    char ch;
    BinTree bt;
    scanf_s("%c",&ch);
    if(ch=='@')
        bt == NULL;
    else
    {
        bt = (BinTreeNode *)malloc(sizeof(BinTreeNode));
        bt->data = ch;
        bt->leftchild = CreateBinTree_Recuision();
        bt->rightchild = CreateBinTree_Recuision();
    }
    return bt;
}

先序遍历

• 真代码

void PreOrder_Recursion(BinTree bt)
{
    if(bt==NULL)
        return;
    printf("%c",bt->data);
    PreOrder_Recursion(bt->leftchild);
    PreOrder_Recursion(bt->rightchild);
}

中序遍历

• 真代码

void InOrder_Recursion(BinTree bt)
{
    if(bt==NULL)
        return;
    InOrder_Recursion(bt->leftchild);
    printf("%c",bt->data);
    InOrder_Recursion(bt->rightchild);
}

后序遍历

• 真代码

void PostOrder_Recursion(BinTree bt)
{
    if(bt==NULL)
        return;
    PostOrder_Recursion(bt->leftchild);
    PostOrder_Recursion(bt->rightchild);
    printf("%c",bt->data);
}

广度（层次）遍历

• 真代码

void LevelOrder(BinTree bt)
{
    BinTree p;
    LinkQueue queue = SetNullQueue_Link();			//创建空队列
    if(bt==NULL)
        return;
    p = bt;
    EnQueue_Link(queue,bt);							//根结点入队
    while(!IsNullQueue_Link(queue))					//队列不空，循环执行
    {
        p = FrontQueue_link(queue);					//取队头
        DeQueue_link(queue);						//出队
        printf("%c",p->data);
        if(p->leftchld!=NULL)
            EnQueue_link(queue.p->leftchild);		//左孩子不空，入队
        if(p->rightchild!=NULL)
            EnQueue_link(queue,p->rightchild);		//右孩子不空，入队
    }
}

（非递归）二叉树的建立于遍历

• 非递归建立二叉树算法思路：

  1. 将二叉树扩充为完全二叉树，输入==完全二叉树序列==，以#为结束标志，设置计数器count为-1，用来标志结点的序号

  2. 如果输入的不是@，则生成一个新的结点s，并对结点的数据域赋值为输入的字符，结点左右指针域为空，结点s入队

     如果输入的是@，@也入队，但不生成新的结点

     count++

  3. 如果count=0，则结点为根结点，设置二叉树的根bt=s

     如果count=奇数，则结点为父结点p（队头结点）的左孩子，即p->leftchild=s；

     如果count=偶数，则结点为父结点p（队头结点）的右孩子，即p->rightchild=s；

     队头结点p处理完毕，出队

• 代码实现：

BinTree CreateBinTree_NRecursion()
{
    LinkQueue queue = SetNullQueue_Link();		//设置空队列
    BinTreeNode *s, *p, *bt;
    char ch;
    int count = -1;
    ch = getchar();
    bt = NULL;		//设置二叉树为空
    while(ch!='#')	//假设结点的值为单个字符，以#结束
    {
        s = NULL;
        if(ch!='@')	//判断读入的点是否为虚结点'@'
        {
            s = (BinTreeNode *)malloc(sizeof(BinTreeNode));		//申请新结点空间
            s->data = ch;		//新结点数据域赋值
            s->leftchild = s->rightchild = NULL;		//新结点左右指针域置空
        }
        EnQueue_link(queue,s);		//新结点地址或虚结点地址入队
        count++;		//计数器++
        if(count == 0)
        {
            bt = s;		//计数器为0，当前结点为根结点
        }
        else
        {
            p = FrontQueue_link;		//取队头元素
            if(s!=NULL&&p!=NULL)		//当前结点和双亲结点都不为虚结点
            {
                if(count%2 == 1)		//count为奇数，新结点为左孩子	
                    p->leftchild = s;
                else p->rightchild = s;		//count为偶数，新结点为右孩子
            }
            if(count % 2 == 0)
            	Dequeue_link(queue);		//两个孩子处理完毕，出队，处理下一个结点
        }
        ch = getchar();
    }
    return bt;
}

先序遍历

• 算法思路一：

让每个结点都进栈出栈一次，先将根结点压入栈中，如果栈不空，弹出一个元素依次访问其右孩子和左孩子，再重复判断栈是否为空，不空则出栈将其右左孩子入栈，直到栈空为止

• 算法实现：

void PreOrder_NRecursion1(BinTree bt)
{
    LinkStack lstack;
    lstack = SetNullStack_Link();
    BinTreeNode *p;
    Push_link(lstack,bt);				//根结点入栈
    while(!IsNullStack_link(lstack))
    {
        p = Top_link(lstack);			//弹出入栈结点进行判断
        Pop_link(lstack);
        printf("%c",p->data);
        if(p->rightchild)
            Push_link(lstack,p->rightchild);		//右子树不空，进栈
        if(p->leftchild)
            Push_link(lstack,p->leftchild);			//左子树不空，进栈
    }
}

• 算法思路一：

右孩子入栈，左孩子直接访问，直到遍历完所有的左孩子，判断栈空，如果不空，弹出，访问右结点，直到栈空

• 算法实现：

void PreOrder_NRecursion2(BinTree bt)
{
    LinkStack lstack;	//定义链栈
    BinTreeNode *p = bt;
    lstack = SetNullStack_Link();	//初始化链栈
    if(bt == NULL)
        return;
    Push_link(lstack,bt);
    while(!IsNullStack_link(lstack))	//当栈不空时
    {
        p = Top_link(lstack);
        Pop_link(lstack);
        while(p)		//当左结点不空时
        {
            printf("%c",p->data);	//访问结点
            if(p->rightchild)
                Push_link(lstack,p->rightchild);
            p = p->leftchild;
        }
    }
}

中序遍历

• 算法思路：

先让所有左分支的结点入栈，然后倒序访问，每访问一个结点过后访问其右子树，如果右子树有内容，则重复让右子树所有结点入栈，直到右子树为空或者栈为空，遍历完成

• 算法实现：

void InOrder)NRecursion1(BinTree bt)
{
    LinkStack lstack;
    lstack = SetNullStack_Link();
    BinTree p;
    p = bt;
    if(p == NULL)
        return;
    Push_link(lstack,bt);		//根结点进栈
    p = p->leftchild;		//访问左子树
    while(p||!IsNullStack_link(lstack))		//当p不空或栈为空时跳出循环
    {
        while(p!=NULL)		//当p不空
        {
            Push_link(lstack, p);	//左子树结点不断进栈
            p = p->leftchild;
        }
        p = Top_link(lstack());		//取栈顶元素访问
        Pop_link(lstack);
        printf("%c",p->data);		
        p = p->rightchild;		//访问结点的右子树
    }
}

后序遍历

• 算法思路：

==访问的第一个结点应该是叶子结点==

先让所有的左分支的结点入栈，然后检查右分支，如果右分支不为空则继续检查右分支的左分支，直到一个结点的左右两分支都为空，该结点出栈，访问

如果该结点是父结点的左孩子，则继续进入父结点的右分支检查右分支的左分支

如果该结点是父结点的右孩子，则访问其父结点，退回到上一层

直到叶子结点为空且栈也空

• 算法实现：

void PostOrder_NRecursion(BinTree bt)
{
    BinTree p = bt;
    LinkStack lstack;
    if(bt == NULL)
        return;
    lstack = SetNullStack_Link();
    while(p!=NULL || !IsNullStack_link(lstack))
    {
        while(p != NULL)
        {
            Push_link(lstack,p);
            p = p->leftchild? p->leftchild:p->rightchild;
        }
        p = Top_link(lstack);
        Pop_link(lstack);
        printf("%c",p->data);
        if(!IsNullStack_link(lstack)&&(Top_link(lstack)->leftchild == p))
            p = (Top_link(lstack))->rightchild;//如果当前结点是父结点的左子树，进入父结点的右子树
        else p = NULL;		//如果当前结点是父结点的右子树，退回到上一结点
    }
}

二叉树的其他操作

统计二叉树叶子结点个数

int CountLeafNode(BinTree bt)
{
    if(bt == NULL)
        return 0;		//递归调用结束条件
    else if((bt->leftchild == NULL)&&(bt->rightchild == NULL))		//如果是叶子结点返回1
        return 1;
    else		//递归遍历左子树和右子树
        return(CountLeafNode(bt->leftchild) + CountLeafNode(bt->rightchild));
}

统计二叉树总的结点个数

int CountNode(BinTree bt)
{
    if(bt == NULL)
        return 0;		//递归调用结束条件
    else return(CountNode(bt->leftchild) + CountNode(bt->rightchild) + 1);
}

统计二叉树右结点数

int CountRightNode(BinTree bt)
{
    int num = 0;
    if(bt == NULL)
        return 0;
    if(bt->rightchild!=NULL)
        num++;
    num += CountRightNode(bt->leftchild);
    num += CountRightNode(bt->rightchild);
    return num;
}

计算二叉树的深度

int CountLevel(BinTree bt)
{
    if(bt == NULL)
        return 0;
    else
    {
        int i = CountLevel(bt->leftchild);
        int j = CountLevel(bt->rightchild);
        return (i>j?i:j) + 1;
    }
}

查找数据元素

有空记得补

树和森林

树、森林转为二叉树

• 加线：在所有相邻的兄弟结点之间连线
• 抹线：对每个非终端结点，只保留它到其最左子女的连线，删去与其他子女的连线
• 调整：以根结点为轴心，将整颗树进行旋转

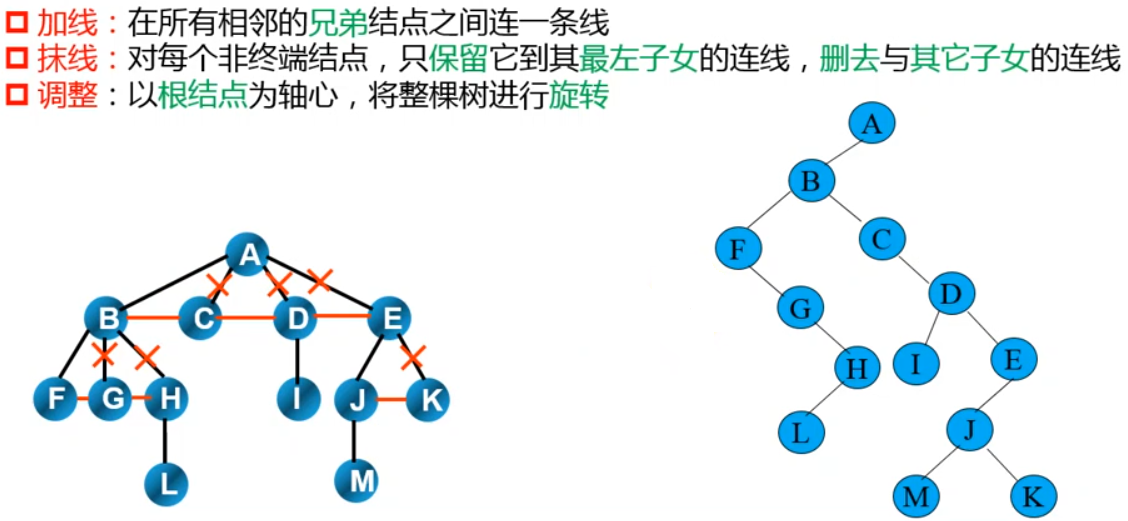
二叉树转换为树或森林

• 加线：若p结点时双亲结点的左孩子，则将p的右孩子，右孩子的右孩子，…，沿分支找到所有的右孩子，都与p的双亲用线相连
• 抹线：抹掉原二叉树中双亲与右孩子之间的连线
• 调整：将结点按层次排列，形成树结构

哈夫曼树

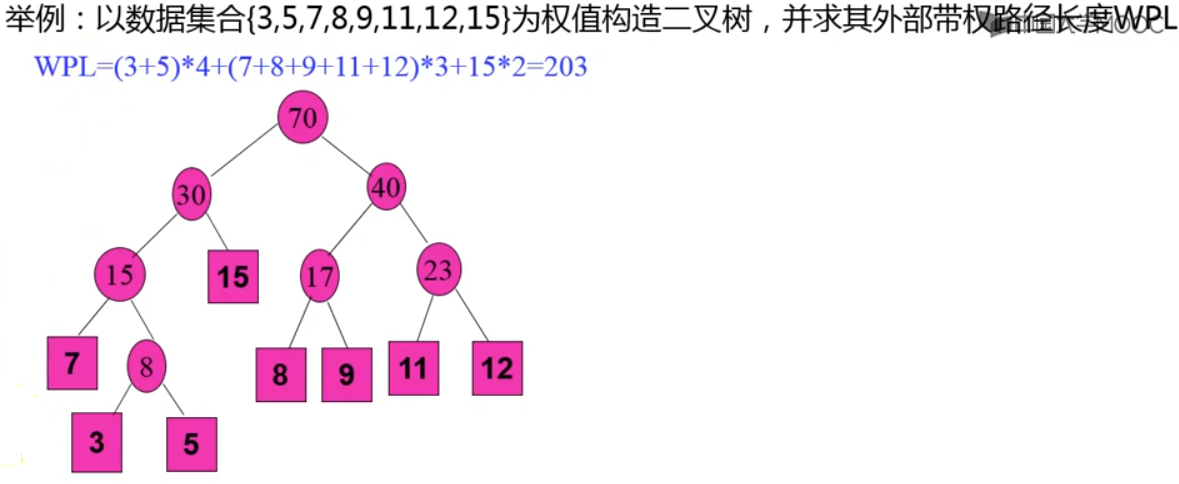
WPL：扩充二叉树的带权的外部路径长度

​ $\displaystyle \sum^{m}_{i \to 0}{w_i \times l_i}$

wi 是第 i 个外部结点的权值， li 是从根到第 i 个外部结点的路径长度，m为外部结点的个数

哈夫曼算法

• 算法思路：

1. 由给定的 m 个权值 {w1，w2，…，wm} 构造成 m 颗二叉树集 F = {T1，T2，…，Tm }，其中每一棵二叉树 Ti 中只有一个带权为 wi 的根结点，且根结点的权值为 wi
2. 在 F 中选取两棵权值最小的树作为左右子树构造一棵新的二叉树，且新二叉树的根结点的权值为其左右子树根结点权值之和
3. 在F中删除这两棵树，同时将新得到的二叉树加入 F 中
4. 重复 2. 和 3. ，直到 F 中只含一棵树为止

• 类型定义：

struct HuffNode
{
    int weight;	//权值
    int parent,leftchild,rightchild;	//父结点与左右孩子
};
typedef struct HuffNode *HtNode;
typedef struct HuffTreeNode
{
    int n;		//哈夫曼树的叶子结点个数
    int root;	//哈夫曼树的树根
    HtNode ht;	//指向哈夫曼树的指针
}*HuffTree;

• 算法实现：

HuffTree CreateHuffTree(int n,int *w)
{
    HuffTree pht;
    int i, j, x1, x2, min1, min2;
    pht = (HuffTree)malloc(sizeof(struct HuffNode)*(2*n-1));
    if(pht == NULL)
    {
        printf("Oui of space!\n");
        return pht;
    }
    //为哈夫曼树申请 2n-1 个空间
    pht->ht = (HtNode)malloc(sizeof(struct HuffNode)*(2*n-1));
    if(pht->ht == NULL)
    {
        printf("Oui of space!\n");
        return pht;
    }
    //初始化哈夫曼树
    for(i = 0;i<2*n-1;i++)
    {
        pht->ht[i].leftchild = -1;		//初始化叶结点的左孩子
        pht->ht[i].rightchild = -1;		//初始化叶结点的右孩子
        pht->ht[i].parent = -1;			//初始化叶结点的父亲
        if(i<n)
            pht->ht[i].weight = w[i];
        else
            pht->ht[i].weight = -1;
    }
    for(i=0;i<n-1;i++)
    {
        min1 = MAX;	//min1代表最小值
        min2 = MAX;	//min2代表次小值
        x1 = -1;	//最小值下标
        x2 = -1;	//次小值下标
        //找到最小值下标 x1 并把最小值赋给 min1
        for(j=0;j<n+1;j++)
        {
            if(pht->ht[j].weight < min1&&pht->ht[j].parent == -1)
            {
                min2 = min1;
                x2 = x1;
                min1 = pht->ht[j].weight;
                x1 = j;
            }
         //找到次小值下标x2并把次小值赋给min2
        	else if(pht->ht[j].weight < min2&&pht->ht[j].parent == -1)
            {
                min2 = pht->ht[j].weight;
                x2 = j;
            }
        }
       	//构建 x1，x2 的父结点
        pht->ht[x1].parent = n+1;	//x1父结点下标
        pht->ht[x2].parent = n+1;	//x2父结点下标
        pht->ht[n + i].weight = min1 + min2;	//父结点的权值为极小值加次小值
        pht->ht[n + i].leftchild = x1;	//父结点的左孩子为x1
        pht->ht[n + i].rightchild = x2;	//父结点的右孩子为x2
    }
    pht->root = 2*n-2;		//哈夫曼树根结点位置
    pht->n = n;
    return pht;
}

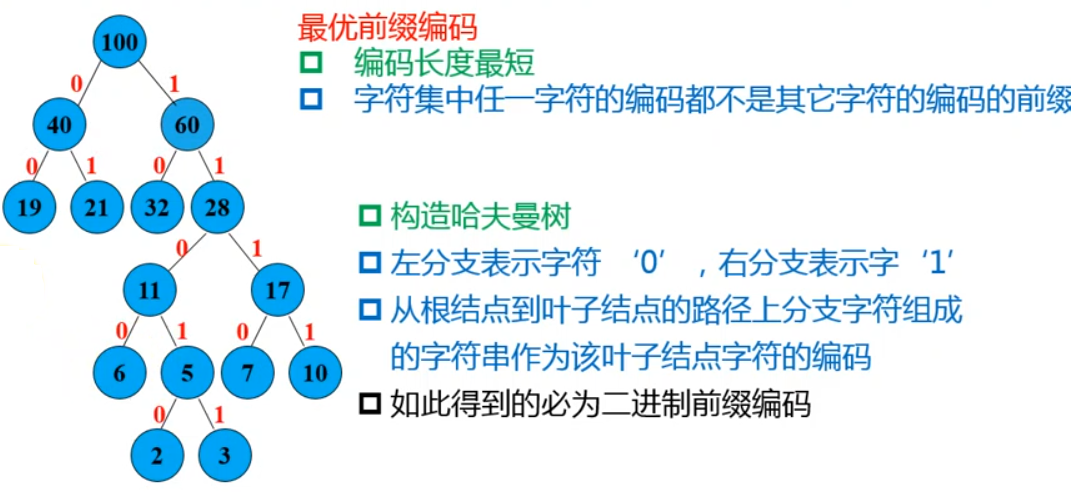
哈夫曼编码（最优前缀编码）

• 编码长度最短
• 字符集中任一字符的编码都不是其他字符的编码的前缀

第四章 搜索树

二分判定查找树

• 平均检索长度：ASL

• 二分查找判定树

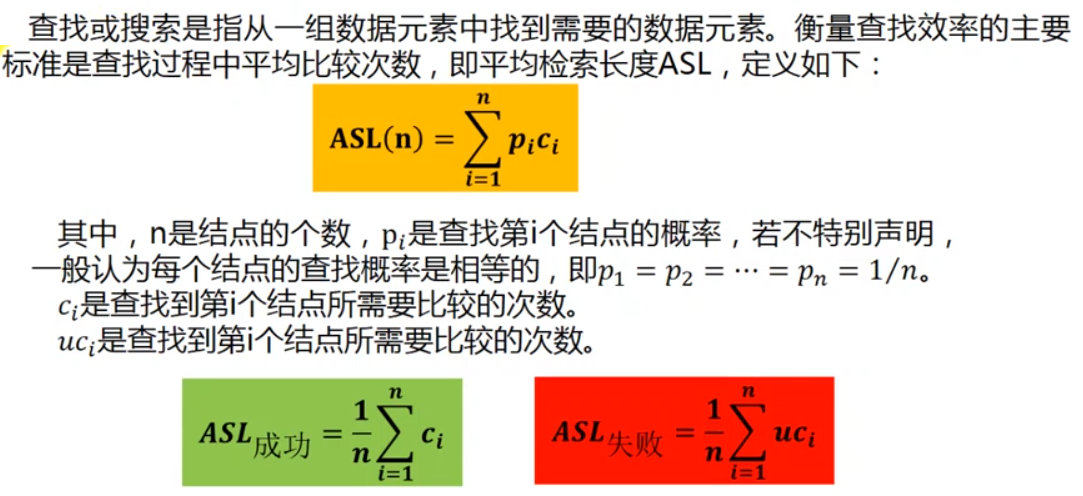
查找成功：查找二分查找判定树中已有的结点，路径为根结点——>该结点，经过结点个数为比较次数

查找失败：走的是一条根结点——>扩充二叉树的外部结点的路径

二分排序树（BST）的基本概念

• ==对称遍历有序性==
• ==二分查找方便==
• ==插入的都是叶子结点==
• ==删除不需要移动结点==

二分排序树的查找

• 返回NULL查找成功，否则查找失败

BSTreeNode BSTearch(BinSearTree bt,DataType key)
{
    BSTreeNode p,parent;
    p = bt;
    parent = p;	//记录待插入结点的父结点
    while(p)
    {
        parent = p;
        if(p->data == key)
        {
            printf("exist this key\n");
            return NULL;
        }
        if(p->data > key)
            p = p->leftchild;
        else
            p = p->rightchild;
    }
    return parent;
}

二分排序树的插入

• 先查询，建立新结点，判断原二叉排序树是否为空，为空则为根结点，否则进入判断，新结点大于父结点插入右子树，新结点小于父结点插入左子树
• 插入成功返回1，失败返回0

int BSTInsert(BinSearTree bt,DataType key)
{
    BSTreeNode p,temp;
    temp = BSTSearch(bt,key);	//调用查找算法，在上面
    if(temp == NULL)
    {
        printf("exist this key\n");
        return 0;
    }
    p = (BSTreeNode*)malloc(sizeof(struct BinSearTreeNode));	//申请结点
    if(p == NULL)
    {
        printf("malloc 失败\n");
        return 0;
    }
    p->data = key;
    p->leftchild = p->rightchild = NULL;
    if(key < temp->data)
        temp->leftchild = p;	//作为左孩子插入
    else
        temp->rightchild = p;	//作为右孩子插入
    return 1;
}

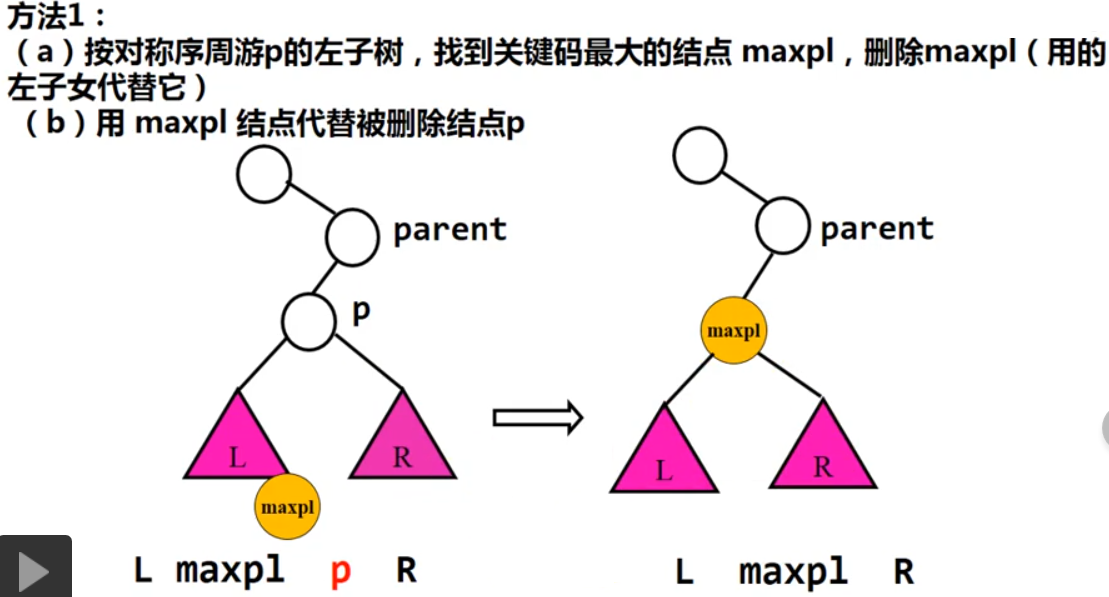
二分排序树的删除

• 如果待删除结点 p 的左子树为空，则只要令右子树的根结点直接代替 p 即可

• 如果待删除结点 p 的左子树不为空

• • 方法一：

  • 需要遍历 p 的左子树，找到最大的结点 maxpl ，删除 maxpl，再用 maxpl 代替 p 原来的位置

  • • 如果 maxpl 有左分支，用其左分支代替原来 maxpl 的位置， maxpl 依旧去代替 p 结点的位置

• 删除算法：

int BSTDelete1(BinSearTree *bt,DataType key)
{
    // parent 记录 p 的父结点，maxpl 记录 p 的左子树中最大的结点
    BSTreeNode parent ,p,maxpl;
    p = *bt;
    parent = NULL;
    while(p!=NULL)
    {
        if(p->data == key)
            break;
        parent = p;
        if(p->data > key)
            p = p->leftchild;
        else
            p = p->rightchild;
    }
    if(p == NULL)
    {
        printf("not exist\n");
        return 0;
    }
    if(p->leftchild == NULL)	//只有右子树的情况
    {
        if(parent == NULL)		//判断是不是删了根结点
            *bt = p->rightchild;
        else if(parent->leftchild == p)		//如果p是父结点的左孩子
            parent->leftchild = p->rightchild;
        else								//如果p是父结点的右孩子
            parent->rightchild = p->rightchild;
    }
    if(p->leftchild!=NULL)	//p有左子树和右子树
    {
        BSTreeNOde parentp;	//parentp记录maxpl的父结点
        parentp = p;
        maxpl = p->leftchild;
        while(maxpl->rightchild != NULL)
        {
            parentp = maxpl;
            maxpl = maxpl->rightchild;
        }
        p->data = maxpl->data;	//修改 p 的数据域为 maxpl 的数据域
        if(parentp == p)		//如果maxpl父结点是p
            p->leftchile = maxpl->leftchild;	//修改p的左指针，置空
        else
            parentp->rightchild = maxpl->leftchild;	//修改父结点的左指针，置空
        p = maxpl;	//更新 p 指针为 maxpl 结点以便删除
    }
    free(p);
    return 1;
}

• • 方法二：
  • 直接让 p 的左子树根结点代替 p ，p 的 右子树接到 maxpl 的右子树

int BSTDelete2(BinSearTree *bt,DataType key)
{
    // parent 记录 p 的父结点，maxpl 记录 p 的左子树中最大的结点
    BSTreeNode parent ,p,maxpl;
    p = *bt;
    parent = NULL;
    while(p!=NULL)
    {
        if(p->data == key)
            break;
        parent = p;
        if(p->data > key)
            p = p->leftchild;
        else
            p = p->rightchild;
    }
    if(p == NULL)
    {
        printf("not exist\n");
        return 0;
    }
    if(p->leftchild == NULL)	//只有右子树的情况
    {
        if(parent == NULL)		//判断是不是删了根结点
            *bt = p->rightchild;
        else if(parent->leftchild == p)		//如果p是父结点的左孩子
            parent->leftchild = p->rightchild;
        else								//如果p是父结点的右孩子
            parent->rightchild = p->rightchild;
    }
    if(p->leftchild!=NULL)	//p有左子树和右子树
    {
        maxpl = p->leftchild;
        while(maxpl->rightchild!=NULL)
            maxpl = maxpl->rightchild;
        maxpl->rightchild = p->rightchild;	//把p的右分支全部接到 maxpl 的右分支，因为都比 maxpl 大
        if(parent == NULL)	//判断是不是删了根结点
            *bt = p->leftchild;
        else if(parent->leftchild == p)		//如果p是父结点的左孩子
            parent->leftchild = p->leftchild;
        else								//如果p是父结点的右孩子
            parent->rightchild = p->leftchild;
    }
    free(p);
    return 1;
}

平衡二叉排序树（AVL）的概念

• 可以是空树
• ==左右子树均为平衡二叉排序树，且左右子树深度之差绝对值不超过1==
• 结点的==平衡因子BF：结点的左子树深度 - 右子树深度==

AVL树

• ==平衡因子BF只能是 -1，0，1 的二叉树==

AVL树的四种调整

以后有空补上

第五章 图

图的基本概念

• 度：无向图中顶点 v 的度是关联与该顶点的边的数目，记为 D(v)

• 入度：有向图中以顶点 v 为终点的边的数目称为 v 的入度，记为 ID(v)

• 出度：有向图中以顶点 v 为始点的边的数目称为 v 的出度，记为 OD(v)

• ==有向图中顶点 v 的度定义为该顶点的入度和出度之和==

• ==无论是有向图还是无向图，顶点数 n 和边数 e 和度数之间的关系为==

​ $\displaystyle \sum^{n}_{i \to 1}{D(v_i) / 2}$

你开始小心翼翼的避开我，像极了曾经的自己，而我能做的只是远远的望着你，其实我也很想主动靠近你，但最后还是把耐心都给了你，时间过了很久你还是不为所动，好像根本就没有意识到我的存在，我开始有些失落，想着是否能够离你近一点，可你那过分的敏感，让我愣在原地有些不知所措，脑海里出现过很多不同的场景，可能是压抑了太久，我觉得自己已经很卑微了，但对于你来说，不知道这是错过还是解脱。但其实说来也好笑，自己又何尝不是和你一样呢。你还是不肯面对我，即使你已经走到了我的面前，你真的已经缺席了太多我需要你的时刻，你曾经那模糊的好感，让我心动很久，可现在，我已经没有再等下去的勇气了，我的心，已经开始乱了。不甘心于舍不得，只会让我们的距离越来越大，原来我始终都是个局外人，这绵延的城市应有尽有，却唯独没有你，也没有尽头，只有我的存在，始终都是违和的，有些事到此为止，就是最好的收场，不是想通了，是算了，就连你唯一一次朝着我走来，也只不过是给了我一场空欢喜，若不是失望到极致，又怎会，两眼无悲喜，你给我的遗憾虽然很多很多，但最后离开的你，也陪我度过了很久很久

图的存储表示

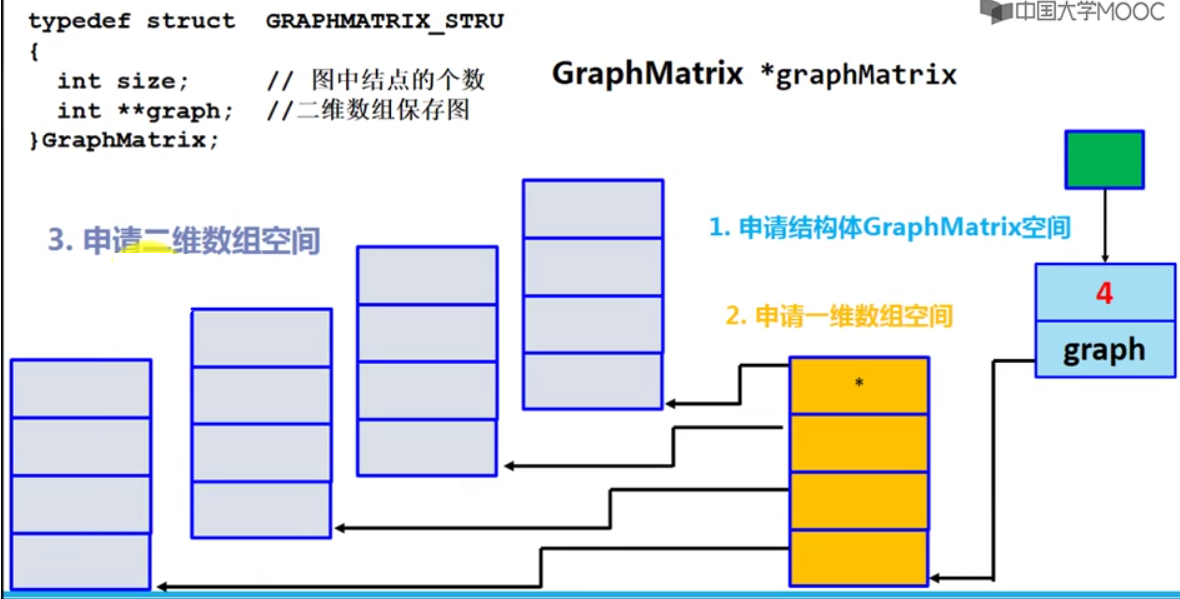
邻接矩阵表示法

举例：

• 邻接矩阵图的类型定义

typedef struct GRAPHMATRIX_STRU
{
    int size;		//图中结点的个数
    int **graph;	//二维数组保存图
}GraphMatrix;

• 初始化图（邻接矩阵）

GraphMatrix* InitGraph(int num)
{
    int i,j;
    GraphMatrix* graphMatrix = (GraphMatrix*)malloc(sizeof(GraphMatrix));
    graphMatrix->size = num;	//图中结点个数
    //给图分配空间
    graphMatrix->graph = (int**)malloc(sizeof(int*)*graphMatrix->size);
    for(i=o;i<graphMatrix->size;i++)
        graphMatrix->graph[i]=(int*)malloc(sizeof(int)*graphMatrix->size);
    for(i=0;i<graphMatrix->size;i++)
    {
        for(j=0;j<graphMatrix->size;j++)
            graphMatrix->graph[i][j] = INT_MAX;	//初始设置所有顶点不邻接
    }
    return graphMatrix;
}

• 为什么要申请两次空间？

• 输入邻接矩阵图算法：

void ReadGraph(GraphMatrix* graphMatrix)	//输入边信息构建图
{
    int vex1,vex2,weight;
    //输入方式是点 点 权值，权值为0，则输入结束
    printf("请输入，输入方式为点 点 权值，权值为0，则输入结束\n");
    scanf_s("%d%d%d",&vex1,&vex2,&weight);
    while(weight!=0)
    {
        graphMatrix->graph[vex1][vex2] = weight;
        scanf_s("%d%d%d",&vex1,&vex2,&weight);
    }
}

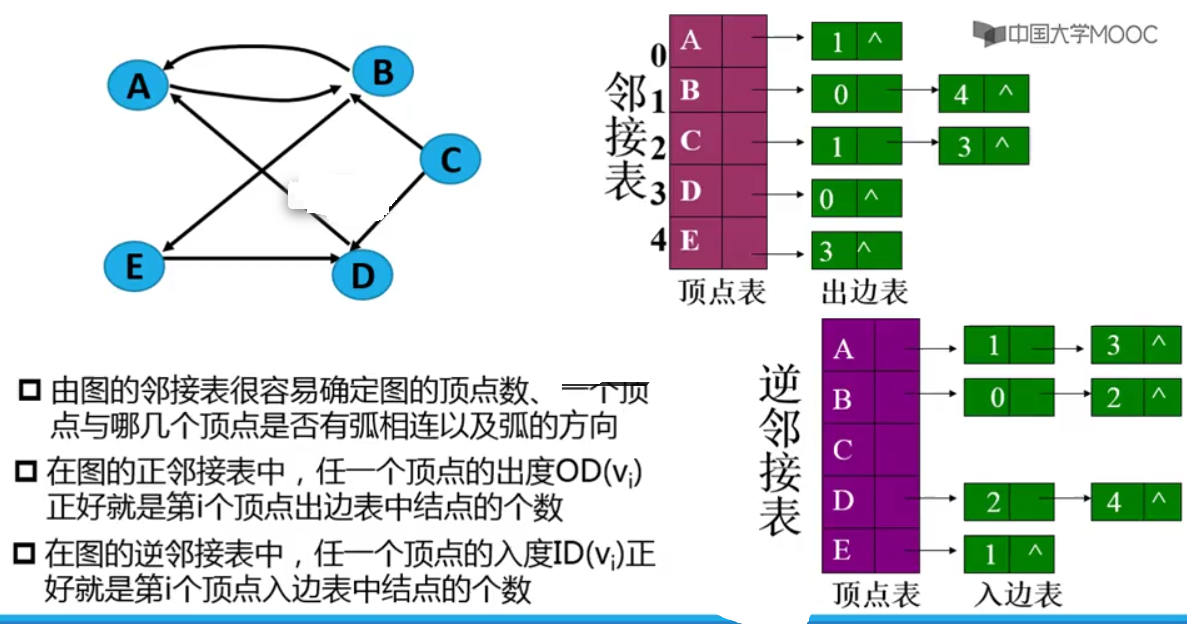
邻接表表示法

举例：

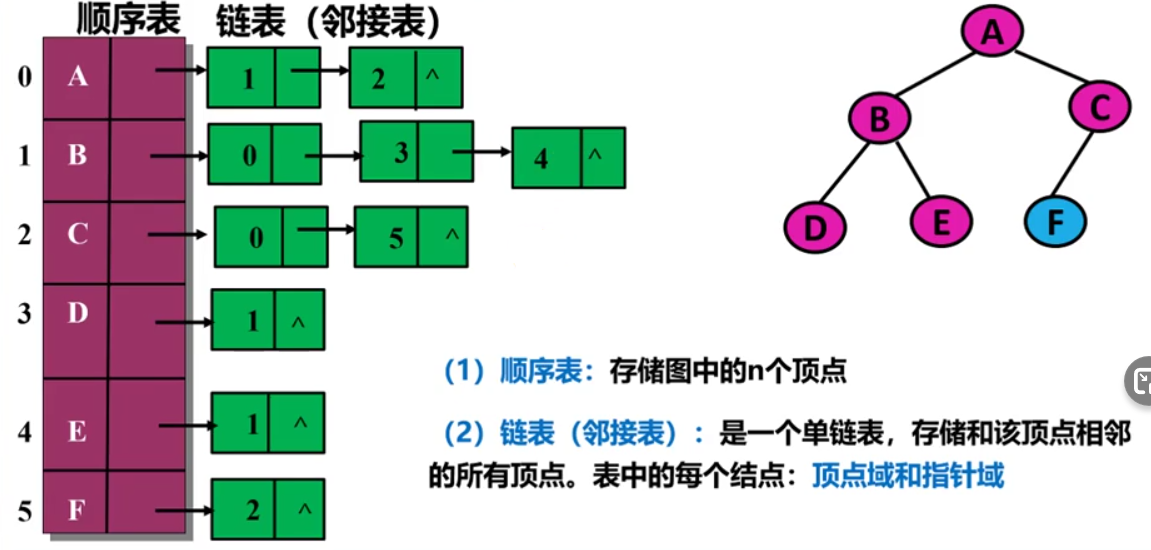
• 容易确定图的顶点数和判断一个顶点与哪几个顶点是否有边相连
• 容易确定图的顶点的度，即顶点对应顺序表的链表链接的结点个数

• 邻接表图的类型定义

typedef struct GRAPHLISTNODE_STRU
{
    int nodeno;	//图中结点编号
    struct GRAPHLISTNODE_STRU* next;	//指向下一个结点的指针
}GraphListNode;

typedef struct GRAPHLIST_STRU
{
    int size;	//图中结点个数
    GraphListNode* graphListArray;	//图的邻接表，用二维数组表示
}GraphList;

• 初始化图（邻接表）

GraphList* IniGraph(int num)
{
    int i;
    GraphList *grahList = (GraphList*)malloc(sizeof(GraphList));
    grapList->size = num;
    graphList->graphListArray = (GraphListNode*)malloc(sizeof(GraphListNode)*num);
    for(i=0;i<num;i++)
    {
        graphList->graphListArray[i].next = NULL;
        graphList->graphListArray[i].nodeno = i;
    }
    return grapList;
}

• 输入邻接矩阵图算法：

void ReadGraph(GraphList* graphList)
{
    int vex1,vex2;
    GraphListNode *tempNode = NULL;
    //输入方式为点 点，点为-1，则输入结束
    printf("请输入，输入方式为点 点，点为-1，则输入结束\n");
    scanf_s("%d%d",&vex1,&vex2);
    while(vex1>=0 && vex2>=0)
    {
        tempNode = (GraphListNode*)malloc(sizeof(GraphListNode));
        tempNode->nodeno = vex2;
        tempNode->next = NULL;
        //头插法插入结点
        tempNode->next = graphList->graphListArray[vex1].next;
        graphList->graphListArray[vex1].next = tempNode;
        scanf_s("%d%d",&vex1,&vex2);
    }
}

邻接多重表表示法

图的十字链表

以后有空补上

图的周游

• 遍历每个顶点，不重复

深度优先搜索（DFS）

• 指定顶点v出发，先访问顶点v，并将其标记
• 如果存在与v邻接顶点没被访问过，则选择其中的一个w出发进行DFS(w)
• 否则，返回
• 如果图中有未被访问的顶点，则从另一未被访问的顶点出发重复上述过程，直到遍历全部顶点
• 邻接矩阵 DFS 算法实现：

void DFSGraphMatrix(GraphMatrix * graphMatrix)
{
    int i;	//用于记录图中结点哪些被访问了
    int *visited = (int*)malloc(sizeof(int)* graphMatrix->size);
    //初始化所有点都未被访问
    for(i=0;i<graphMatrix->size;i++)
        visited[i] = 0;
    for(i=0;i<graphMatrix->size;i++)
    {
        if(!visited[i])
            DFS(graphMatrix, visite, i);
	}
}
void DFS(GraphMatrix* graphMatrix,int *visited,int source)
{
    int j;
    visited[source] = 1;
    for(j=0;j<graphMatrix->size;j++)
    {
        if(graphMatrix->graph[source][j] != INT_MAX && !visited[j])
            DFS(graphMatrix,visited,j);
    }
}

• 邻接表 DFS 算法实现：

void DFSGraphMatrix(GraphList * graphList)
{
    int i;	//用于记录图中结点哪些被访问了
    int *visited = (int*)malloc(sizeof(int)* graphList->size);
    //初始化所有点都未被访问
    for(i=0;i<graphList->size;i++)
        visited[i] = 0;
    for(i=0;i<graphList->size;i++)
    {
        if(!visited[i])
            DFS(graphList, visite, i);
	}
}
void DFS(GraphLIst* graphList, int* visited,int source)
{
    int j;
    GraphList弄得*tempnode = NULL;
    visited[source] = 1;
    printf("%d",source);
    tempNode = graphList->graphListArray[source].next;
    while(tempNode != NULL)
    {
        if(!visited[tempNode->nodeno])
            DFS(graphList,visited,tempNode->nodeno);
        tempNode = tempNode->next;
    }
}

广度优先搜索（BFS）

• 指定顶点v出发，先访问顶点v，并将其标记
• 依次访问v的所有相邻结点
• 再依次访问与相邻结点邻接的所有没被访问过的顶点
• 直到所有已访问顶点的相邻结点都被访问过为止
• 如果图中有未被访问的顶点，则从另一未被访问的顶点出发重复上述过程，直到遍历全部顶点
• 邻接矩阵 BFS 算法实现：

void BFSGraphMatrix(GraphMatrix * graphList)
{
    int i;	//用于记录图中结点哪些被访问了
    int *visited = (int*)malloc(sizeof(int)* graphList->size);
    //初始化所有点都未被访问
    for(i=0;i<graphList->size;i++)
        visited[i] = 0;
    for(i=0;i<graphList->size;i++)
    {
        if(!visited[i])
            BFS(graphList, visite, i);
	}
}
void BFS(GraphMatrix* graphMatrix,int*visited,int source)
{
    int j,tempVex;
    LinkQueue waitingQueue = NULL;
    waitingQueue = SetNullQueue_Link();
	if(!visited[i])	//如果没被访问过
    {
        visited[i] = 1;
        printf("%d",i);
        EnQueue_link(waitingQueue,i);	//将刚访问结点放入队列
        while(!IsNullQueue_Link(waitingQueue))
        {
            tempVex = FrontQueue_link(waitingQueue);
            DeQueue_link(waitingQueue);
            for(j=0;j<graphMatrix->size;j++)
            {
                //如果其他顶点与当前顶点存在边且未访问过
                if(graphMatrix->graph[tempVex][j] != INT_MAX && !visited[j])
                {
                    visited[j] = source;	//标记
                    EnQueue_link(waitingQueue,j);	//入队
                    printf("%d",j);	//输出
                }
            }
        }
    }
}

• 邻接表 BFS 算法实现

void BFSGraphMatrix(GraphList * graphList)
{
    int i;	//用于记录图中结点哪些被访问了
    int *visited = (int*)malloc(sizeof(int)* graphList->size);
    //初始化所有点都未被访问
    for(i=0;i<graphList->size;i++)
        visited[i] = 0;
    for(i=0;i<graphList->size;i++)
    {
        if(!visited[i])
            DFS(graphList, visite, i);
	}
}
void BFS(GraphList* graphList,int* visited,int source)
{
    int tempVex;
    GraphListNode *tempNode = NULL;
    queue<int> waitingQueue;	//广度优先遍历使用的队列是c++的STL中的queue
    if(!visited[source])
    {
        visited[source] = 1;
        printf("%d",source);
        waitingQueue.push(source);	//刚刚访问结点放入队列
        while(!waitingQueue.empty())
        {
            tempVex = waitingQueue.front();
            waitingQueue.pop();
            tempNode = graphList->graphListArray[tempVex].next;
            while(tempNode != NULL)
            {
                if(!visited[tempNode->nodeno])
                {
                    visited[tempNode->nodeno] = 1;
                    waitingQueue.push(tempNode->nodeno);
                    printf("%d",tempNode->nodeno);
                }
                tempNode = tempNode->next;
            }
        }
    }
}

最小生成树（MST）

Prim算法

• 算法思路：每次选择一条权值最小的边及其相应的顶点加入最小生成树，顶点不能重复选用，直到最小生成树中有 n-1 条边为止

• component[j]用来记录已加入最小生成树的顶点 j，初始化component[j] = 0，当顶点j加入最小生成树后，设置component[j] = 1

• distance[j]用来记录代价最小的边的权值，初始化distance[j] = garphMatrix->graph[0][j]

• neighbor[j]用来记录代价最小的边对应的顶点，初始化neighbor[j] = 0

• 算法实现：

GraphMatrix* prim(GraphMatrix *graphMatrix,int source)
{
    int i,j;
    int *component = (int*)malloc(sizeof(graphMatrix->size));		//新点集合
    int *diftance = (int*)malloc(sizeof(graphMatrix->size));	//距离
    //邻居，例如 neighbor[j] = 1 表示 j 的邻居是 1
    int *neighbor = (int*)malloc(sizeof(graphMatrix->size));
    GraphMatrix *tree = IniGraph(graphMatrix->size);	//存放结果的图
    for(j=0;j<graphMatrix->size;j++)
    {
        component[j] = 0;
        distance[j] = graphMatrix->graph[source][j];
        neighbor[j] = source;
    }//end 9
    component[source] = 1;
    for(i=1;i<graphMatrix->size;i++)
    {
        int v;
        int min = MAX;
        for(j=0;j<graphMatrix->size;j++)	//选择不是新点集合中的距离新点集合最短的那个点
        {
            if（!component[j] && (distance[j]<min))
            {
                v = j;
                min = distance[j];
            }
        }//end 20
        if(min<MAX)
        {
            component[v] = 1;
            tree->graph[v][neighbor[v]] = distance[v];
            tree->graph[neighbor[v]][v] = distance[v];
            for(j=0;j<graphMatrix->size;j++)
            {
                if(!component[j] && (graphMatrix->graph[v][j]<distance[j]))
                {
                    distance[j] = graphMatrix->graph[v][j];
                    neighbor[j] = v;
                }
            }//end 34
        }
        else break;
    }//end 16
    return tree;
}

Kruskai算法

• 算法思路：先把所有顶点加入最小生成树，然后选择合适的边构建最小生成树，边的权值最小且两个点要属于两个不同的连通分量，直到最小生成树中有 n-1 条边为止

typedef struct EDGE_STRU
{
    int begin;	//边的起点
    int end;	//边的终点
    int weight; //边的权值
}Edge;
GraphMatrix* kruskal(GraphMatrix *graphMatrix)
{
    int i,j,k;
    int edgeNum = 0;
    Edge *edge = NULL;
    Edge tempEdge;	//给边排序时的临时变量
    int pos;	//记录添加到哪条边
    int *group;	//记录点是否属于同一连通分量
    int changeGroup;	//记录要变化的连通值
    GraphMatrix * tree = IniGraph(graphMatrix->size);	//存放结果的图
    group = (int*)malloc(sizeof(int)*graphMatrix->size);
    for(i=0;i<graphMatrix->size;i++)	//初始化，点之间不连通
        group[i] = i;
    //分析有多少条边
    for(i=0;i<graphMatrix->size;i++)
    {
        for(j=i+1;j<graphMatrix->size;j++)
        {
            if(graphMatrix->graph[i][j]<INT_MAX)
                edgeNum++;
        }
    }
    //根据刚计算出来的边的数量分派空间
    edge = (Edge*)malloc(sizeof(Edge)*edgeNum);
    k = 0;	//给边赋值的时候用
    for(i=0;i<graphMatrix->size;i++)
    {
        for(j=1;j<graphMatrix->size;j++)
        {
            if(graphMatrix->graph[i][j]<INT_MAX)
            {
                edge[k].begin = i;
                edge[k].end = j;
                edge[k].weight = graphMatrix->graph[i][j];
                k++
            }
        }
    }
    for(i=0;i<edgeNum;i++)	//根据边权值进行排序
    {
        for(j=i+1;j<edgeNum;j++)
        {
            if(edge[i].weight>edge[j].weight)
            {
                tempEdge = edge[i];
                edge[i] = edge[j];
                edge[j] = tempEdge;
            }
        }
    }
    //每次从边数组中取出最小的一条边，判断是否能添加到最小生成树中
    //边数组已排好序
    for(i=0;i<edgeNum;i++)
    {
        //只添加终点和七点属于两个不同连通分量的边
        if(group[edge[i].begin]!=group[edge[i].end])
        {
            //添加到树中
            tree->graph[edge[i].begin][edge[i].end] = edge[i].weight;
            tree->graph[edge[i].end][edge[i].begin] = edge[i].weight;
            //更新所有跟终点属于同一连通分量的点的连通性
            changeGroup = group[edge[i].end];
            for(j=0;j<edgeNum;j++)
            {
                if(group[j] == changeGroup)
                    group[j] = group[edge[i].begin];
            }
        }
    }
    return tree;
}

Dijstra算法

• 算法实现：

int* dijkstra(GraphMatrix * graphMatrix,int source)
{
    int i,j,vex,min;
    //found数组用于记录哪些点是新点集合的，哪些不是
    int* found = (int*)malloc(sizeof(int)*graphMatrix->size);
    //距离数组，在算法过程中不断更新，最后结果也在这
    int* distance = (int*)malloc(sizeof(int)*graphMatrix->size);
    int* path = (int*)malloc(sizeof(int)*graphMatrix->size);
    for(i=0;i<graphMatrix->size;i++)
    {
        found[i] = 0;
        path[i] = 0;
        distance[i] = graphMatrix->graph[source][i];
    }//end 9
    //将起点加入新点集合中
    found[source] = 1;
    distance[source] = 0;
    //每次加入一个点到新点集合中，规则是当前距离最小的
    for(i=0;i<graphMatrix->size;i++)
    {
        min = MAX;	//寻找距离最小的点
        for(j=0;j<graphMatrix->size;j++)
        {
            if(!found[j] && (distance[j]<min))
            {
                vex = j;
                min - distance[j];
            }
        }//end 22
        found[vex] = 1;	//找到的点加入新点集合
        for(j=0;j<graphMatrix->size;j++)
        {
            if(!found[j] && graphMatrix->graph[vex][j]!=MAX)
            {
                if(min+graphMatrix->graph[vex][j]<distance[j])
                {
                    distance[j] = min + graphMatrix->graph[vex][j];
                    path[j] = vex;
                }
            }
        }//end 31
    }//end 19
    return distance;
}

拓扑排序（AOV网）

• 有向图
• 无环图
• 定点表示活动
• 边表示活动间的先后关系
• 排序方法
  • 从AOV网中选择一个入度为0的顶点输出
  • 在AOV网中删除此顶点和它的所有出边
  • 反复到输出所有顶点

AOV网的拓扑序列不唯一

有回环不存在拓扑序列

• 算法思路：
  • 计算各个顶点的入度
  • 将入度为0的顶点入栈
  • 如果栈不空，取出元素 v 并输出
  • 检查顶点 v 的出边表，将出边表中的每个顶点 w 的入度减一，如 w 的入度为 0 ，顶点 w 入栈
  • 重复直到栈空

int topologicalsort(GraphList *graphList)
{
    int i;
    int count = 0;
    int nodeNum;
    int success = 1;
    stack<int>nodeStack;
    //使用STL中的stack
    GraphListNode *tempNode = NULL;
    int *inPoint = (int*)malloc(sizeof(int)*graphList->size);
    for(i=0;i<graphList->size;i++)
        inPoint[i] = 0;
    for(i=0;i<graphList->size;i++)	//计算顶点的入度
    {
        tempNode = graphList->graphListArray[i].next;
        while(tempNode!=NULL)
        {
            inPoint[tempNode->nodeno]++;
            tempNode = tempNode->next;
        }
    }
    for(i=0;i<graphList->size;i++)
    {
        if(inPoint[i] == 0)
            nodeStack.push(i)
    }
    while(!nodeStack.empty())
    {
        nodeNum = nodeStack.top();
        printf("%d",nodeNum);
        nodeStack.pop();
        count++;
        //检查v的出边，将每条出边的终端顶点的入度 -1 ，若该顶点的入度为 0 ，入栈
        tempNode = graphList->graphListArray[nodeNum].next;
        while(tempNode!=NULL)
        {
            inPoint[tempNode->nodeno]--;
            if(inPoint[tempNode->nodeno]==0)
                nodeStack.push(tempNode->nodeno);
            tempNode = tempNode->next;
        }
    }
    if(count!=graphList->size)
        success = 0;
    return success;
}

关键路径（AOE网）

• 带权的有向图
• 顶点表示时间，有向边表示活动
• 边上的权值表示活动持续的时间
• 顶点所表示的事件实际上就是它的入边所表示的活动都已完成，它的出边所表示的活动可以开始这样一种状态
• 只有一个入度为 0 的顶点
• 只有一个出度为 0 的顶点

具体算法以后再补

六度空间

有空再学，现在不感兴趣——12.18

中国邮递员问题

有空再学，现在不感兴趣——12.18

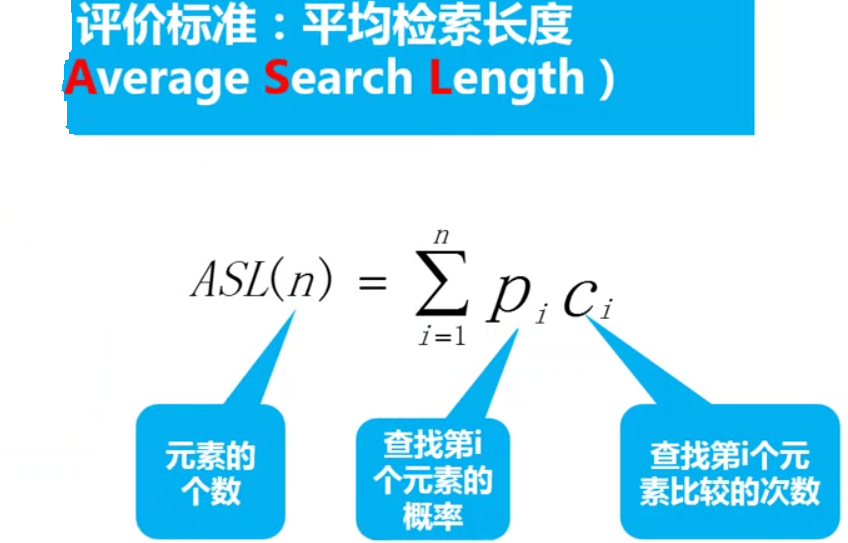
第七章 字典

字典最重要的就是检索

跳跃链表

基本概念

跳跃链表就是在结点中增加指针域，让其直接指向其他的后继结点的指针，使得访问链表的过程中可以交替跳过其直接后继结点

建立和查找

• 类型定义

#define MAX_LEVEL 6	//定义最大层数
typedef int KeyType
//跳跃链表结点结构定义
typedef struct node
{
    int level;	//结点层数
    KeyType key;	//结点的值
    struct node *next[MAX_LEVEL];	//指针数组
}*PNode;
//跳跃链表结构定义
typedef struct
{
    int num;	//跳跃链表数据个数
    int maxLevel;	//跳跃链表最大层数
    PNode head;	//跳跃链表的头指针
}*SkipList;

• 建立

SkipList SetNullSkipList(int level)
{
    SkipList list = (SkipList)malloc(sizeof(SkipList));
    if(list == NULL)
        return NULL;
    list->num = 0;	//跳跃链表计数器置零
    list->maxLevel = level;	//跳跃链表层数
    list->head = CreateNode(level,-1);
    if(list->head == NULL)
    {
        free(list);
        return NULL;
    }
    for(int i = 0;i<level;i++)
    {
        list->head->next[i] = NULL;
    }
    return list;
}

PNode CreateNode(int level,KeyType key)		//生成一个新结点
{
    PNode p = (PNode)malloc(sizeof(PNode) + sizeof(PNode)*level);
    if(p == NULL)
        return NULL;
    p->level = level;
    p->key = key;
    return p;
}

• 查找

PNode SkipListSearch(SkipList list,KeyType key)	//按值查找
{
    int n = 0;
    PNode p = NULL;
    q = NULL;
    p = list->head;
    for(int i =list->maxLevel -1;i>=0;i--)
    {
        while((q = p->next[i]) && (q->key <= key))	//横向比较
        {
            p = q;
            n++;
            if(p->key == key)
            {
                printf("%d\n",n);
                return p;
            }
        }
    }
    return NULL;
}

插入和删除

有空补

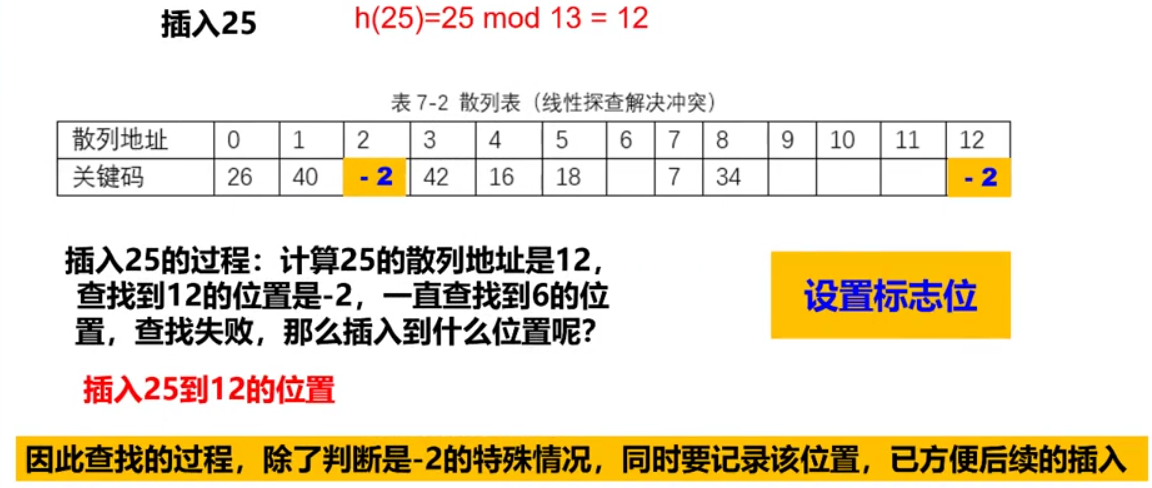
散列表

散列函数和冲突

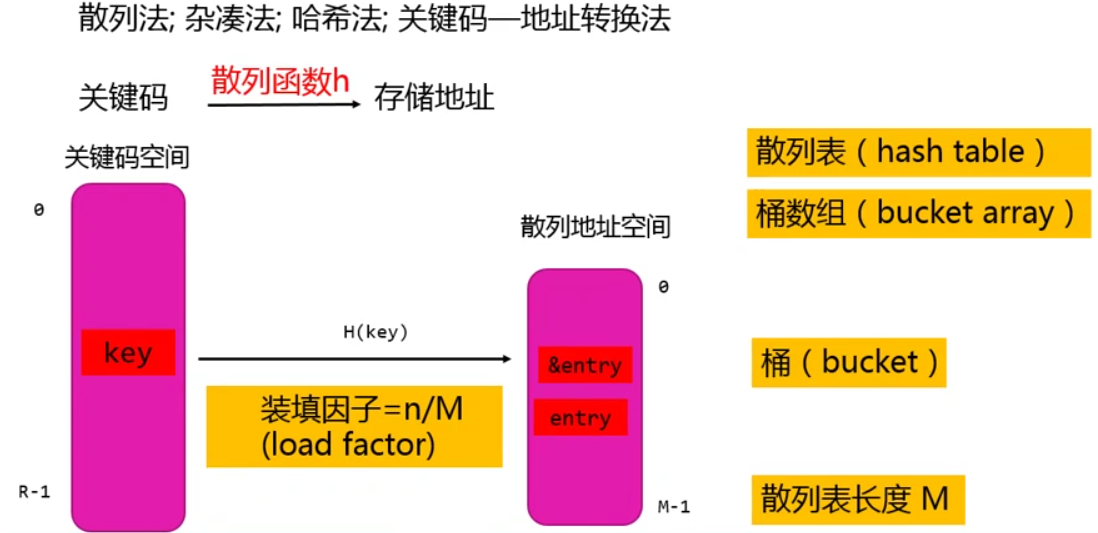
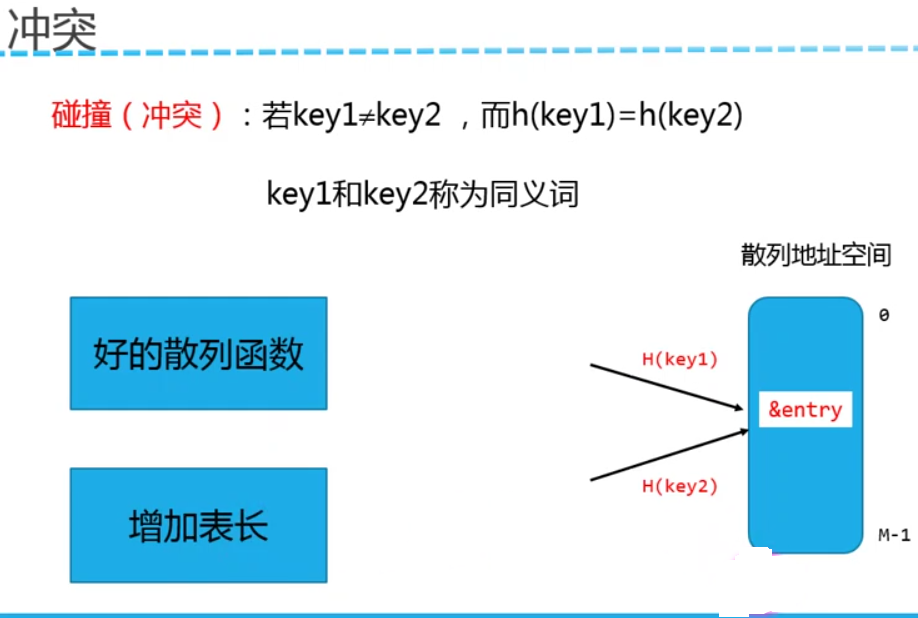
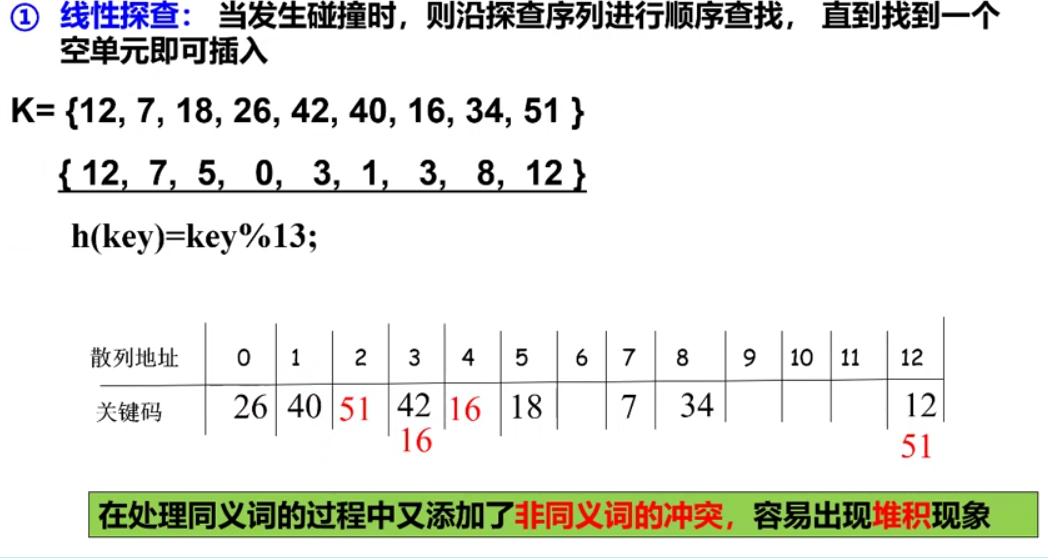
散列表的建立、查找、插入和删除

• 查找

• 插入

• 删除

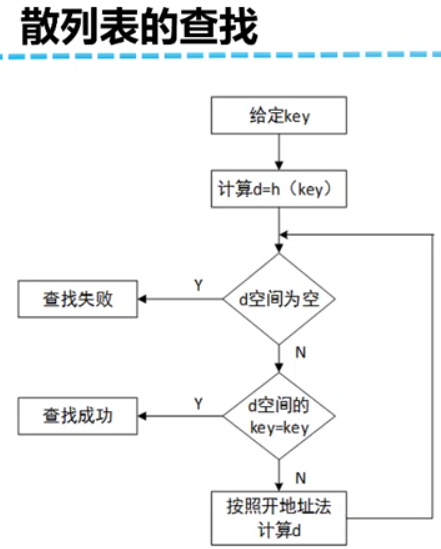
第九章 排序

• 待排序的记录，采用顺序存储结构

typedef int KeyType;
typedef int InfoType;
typedef struct RECORDTYPE_STRU
{
    KeyType key;	//关键字
    InfoType otherInfo;	//其他数据信息
}RecordType;
typedef struct SORTARRAY_STRU
{
    int cnt;	//记录排序数组中元素个数
    RecordType *recordArr;	//指向一维数组的指针
}SortArr;

• 交换函数

void Swap(SortArr* sortArr,int i,int j)
{
    KeyType temp;
    temp = sortArr->recordArr[i].key;
    sortArr->recordArr[i].key = sortArr->recordArr[j].key;
    sortArr->recordArr[j].key = temp;
}

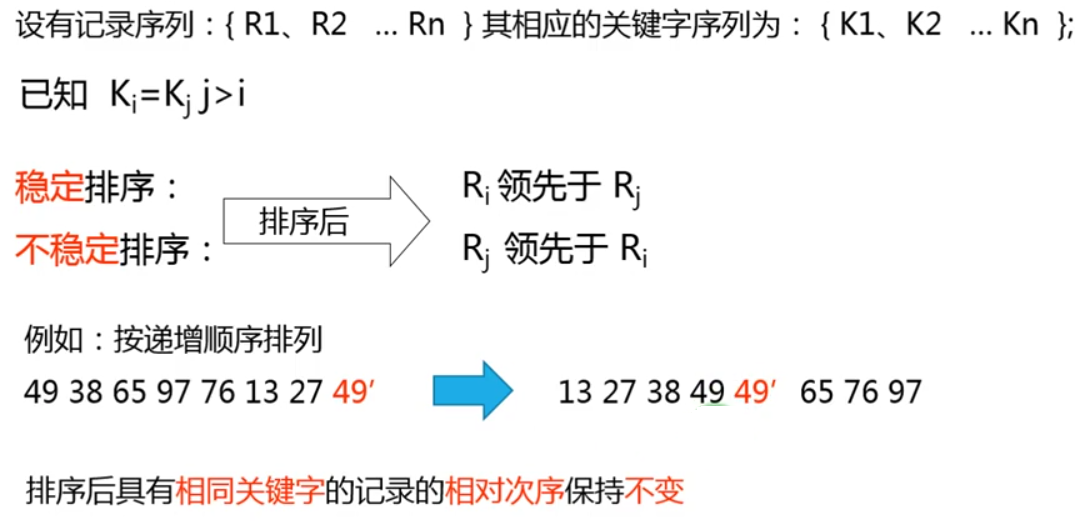
插入类排序

直接插入排序

void InsertSort(SortArr* sortArr)
{
    int i,j;
    RecordType temp;
    for(i = 1;i<sortArr->count;i++)
    {
        j = i - 1;	//j是已经排好顺序的数据最后一个元素的下标
        temp = sortArr->recordArr[i];	//等待插入的数据temp
        //从j位置开始，从后向前在已经排好顺序的序列中找到插入位置
        while(temp.key<sortArr->recordArr[j].key && j>=0)
        {
            sortArr->recordArr[j+1] = sortArr->recordArr[j];	//待插入元素比有序序列中元素小，有序序列中元素往前移
            j--;
        }
        //找到待插入位置为 j+1
        //如果待插入位置正好就是要插入元素所在位置则可以不进行数据赋值
        if((j+1) != i)
            sortArr->recordArr[j+1] = temp;
    }
}

• 算法是稳定的
• 适用于n较小的序列

二分插入排序

void BinSort(SortArr* sortArr)
{
    int i,j;
    int low,mid,high;
    RecordType temp;
    for(i = 1;i<sortArr->count;i++)
    {
        temp = sortArr->recordArr[i];
        low = 0;
        high = i - 1;	//区分左右边界
        while(low <=high)
        {
            mid = (low + high)/2;
            if(temp.key <sortArr->recordArr[mid].key)
                high = mid - 1;	//待排序的值比中间位置的值小，在前半区查找
            else
                low = mid + 1;
        }
        //如果待插入数据正好在还要插入的位置上就不用插入
        if(low != i)
        {
            //如果需要挪动数据，空出位置，插入数据
            //找到插入位置后，移动数据，空出位置
            for(j = i - 1;j>=low;j--)
                sortArr->recordArr[j+1] = sortArr->recordArr[j];
            sortArr->recordArr[low] = temp;	//插入数据
        }
    }
}

• 算法是稳定的
• 链表无法折半

表插入排序

以后有空补

希尔排序

void ShellSort(SortArr* sortArr,int d)
{
    int i,j,increment;	//increment记录当前躺的增量
    RecordType temp;	//保存待排序记录
    for(increment = d;increment>0;increment /= 2)
    {
        for(i = increment;i<sortArr->count;i++)
        {
            temp = sortArr->recordArr[i];	//保存待排序记录
            j = i - increment;	//j按照增量进行变化
            while(j>=0 && temp.key<sortArr->recordArr[j].key)
            {
                //记录按照增量间隔向后移动
                sortArr->recordArr[j+increment] = sortArr->recordArr[j];
                j -= increment;	//j按照增量进行变化
            }
            sortArr->recordArr[j+increment] = temp;	//插入待排序记录
        }
    }
}

• 算法是不稳定的

选择类排序

直接选择排序

void SelectSort(SortArr* sortArr)
{
    int i,j;
    int minPos;	//记录最小元素的下标
    for(i=0;i<sortArr->count-1;i++)	//n-1躺的选择排序
    {
        minPos = i;		//记录最小的值所在的数组下标
        for(j = i+1;j<sortArr->count;j++)	//在无序区域中寻找
        {
            if(sortArr->recordArr[j].key < sortArr->recordArr[minPos].key)
                minPos = j;
        }
        if(minPos != i)	//说明需要交换
            Swap(sortArr,minPos,i);	//调用交换函数
    }
}

• 算法是不稳定的

堆排序

• 根结点大于其左右孩子——大根堆
• 根结点小于其左右孩子——小根堆

后面再补

交换类排序

冒泡排序

//此算法为冒小泡，每次把最小的移动到最左边
void BubbleSort(SortArr *sortArr)
{
    int i,j;
    int hasSwap = 0;	//标志，用于检测内循环是否还有数据交换
    for(i = 1;i<sortArr->count;i++)
    {
        hasSwap = 0;	//每趟开始重新设置交换标志为 0 
        //j是从后往前循环，数组的下标是 0 到 count - 1
        for(j = sortArr->count - 1;j>=i;j--)
        {
            //若前者大于后者
            if(sortArr->recordArr[j-1].key>sortArr->recordArr[j].key)
            {
                Swap(sortArr,j,j-1);
                hsaSwap = 1;	//有交换则设置为 1
            }
        }
    }
    if(!hasSwap)	//本躺没有发生交换
        break;
}

• 算法是稳定的

快速排序

void quickSort(SortObject *pvector,int l,int r)
{
    int i,j;
    RecordNode temp;
    if(l>=r)	//只有一个记录或无记录，不用排序
        return;
    i = l;
    j = r;
    temp = pvector->record[i];	//把枢轴放到temp里面
    while(i!=j)
    {
        while((pvector->record[j].key >= temp.key) && (j>i))
            j--;	//从右向左扫描，直到查找到第一个小于temp.key的记录
        if(i<j)
            pvector->record[i++] = pvector->record[j];
        while((pvector->record[i].key <= temp.key) && (j>i))
            i++;
        if(i<j)
            pvector->record[j--] = pvector->record[i];
    }
    pvector->record[i] = temp;
    quickSort(pvector,l,i-1);
    quickSort(pvector,i+1,r);
}

• 算法是不稳定的

分配类排序

基数排序

以后有空补

归并类排序

两路归并

以后有空补

多路归并

以后有空补